2.2. Функция Грина для слоя диэлектрика на металле
2.2.1. Постановка задачи
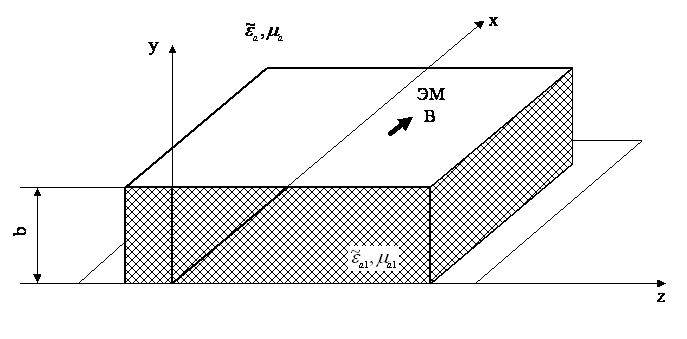
Рассмотрим простую структуру,
образованную металлической плоскостью, покрытой слоем диэлектрика постоянной
толщины b с однородными параметрами ![]() (рис. 2.2.1). Внутри слоя находится параллельный
металлической плоскости элементарный магнитный вибратор. Устройство расположено
в пространстве с однородными параметрами
(рис. 2.2.1). Внутри слоя находится параллельный
металлической плоскости элементарный магнитный вибратор. Устройство расположено
в пространстве с однородными параметрами ![]() . Считаем, что eа1>eа, mа1>mа. Необходимо найти возбуждаемое вибратором электромагнитное
поле. Последнее должно удовлетворять уравнениям Максвелла в слое диэлектрика и
в окружающем пространстве, граничным условиям на металлической поверхности и на
поверхности раздела диэлектриков и, наконец, условиям излучения.
. Считаем, что eа1>eа, mа1>mа. Необходимо найти возбуждаемое вибратором электромагнитное
поле. Последнее должно удовлетворять уравнениям Максвелла в слое диэлектрика и
в окружающем пространстве, граничным условиям на металлической поверхности и на
поверхности раздела диэлектриков и, наконец, условиям излучения.
Введем декартовую систему координат и расположим ее так, чтобы ось х была параллельна вибратору, а плоскость у=0 совпадала с металлической плоскостью. Координаты вибраторов обозначим через х0, у0, z0. Тогда
![]() .
.
Обозначим через Е1, Н1 и Ам1 векторы электрического и магнитного полей и магнитный векторный потенциал, возбуждаемые сторонним источником в слое диэлектрика, то есть при 0£у£b, а через Е, Н и Ам – векторы электрического и магнитного полей и магнитный векторный потенциал в верхнем полупространстве (при у³b). Если считать металлическую плоскость идеально проводящей, то в соответствии с граничным условием
![]() .
.
Имеем
![]() . (1)
. (1)
На поверхности раздела диэлектриков из условия
![]() ,
,
получаем
![]() (2)
(2)
Это есть граничные условия для искомого электромагнитного поля.
Поскольку ![]() , то Аэ1=0 , Аэ=0. Вектор
, то Аэ1=0 , Аэ=0. Вектор ![]() содержит только одну составляющую
содержит только одну составляющую ![]() , поэтому Ам1=ixAмx1, Ам=ixAмx. Функция Aмx1 удовлетворяет неоднородному уравнению Гельмгольца
, поэтому Ам1=ixAмx1, Ам=ixAмx. Функция Aмx1 удовлетворяет неоднородному уравнению Гельмгольца
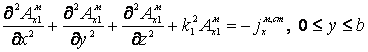 , (3)
, (3)
где ![]() .
.
Поскольку в области у³b сторонних источников нет, то функция Амх удовлетворяет однородному уравнению Гельмгольца
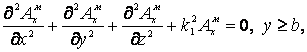 (4)
(4)
где ![]() .
.
Составляющими векторов Е1, Н1 и Е, Н, касательными металлической поверхности и поверхности раздела диэлектриков, являются Ех1, Еz1, Нх1, Нz1, Ех, Еz, Нх, Нz. Определяем их по формулам
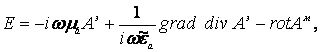
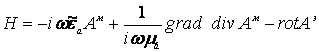
Ех1=Ех=0, Нz1=Hz=0, 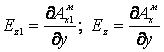 , (5)
, (5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.