Функция Грина для слоя диэлектрика на металле, страница 4

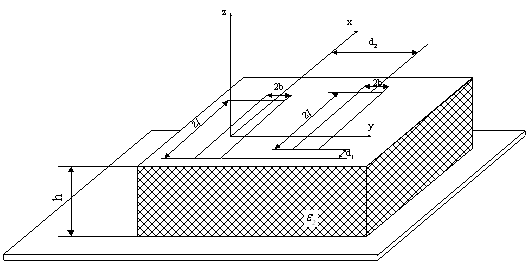
точки М и М₀ – точки наблюдения и интегрирования.

Для нашего случая (рис. 2.2.2) горизонтальных диполей

,

где                        ,                      (5)

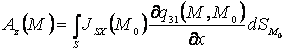                        ,                  (6)

где   - элементы тензора Грина (4)

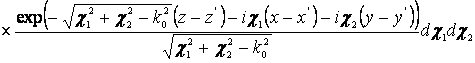 ,    (7)

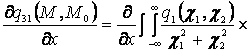
 ,   (8)

,

,

где R_H  и R_E – коэффициенты отражения для Н и Е волн соответственно, определяются из следующих соотношений

,                               (9)

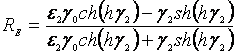,                            (10)

где 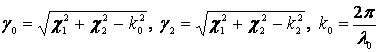 - волновое число свободного пространства,   - волновое число диэлектрика.

Геометрия задачи

Рис. 2.2.2

Подставляя соотношения (3)-(10) в выражение (2), получим

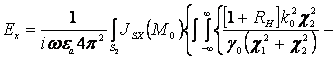
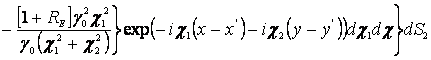          .    (11)

Распределение тока на излучателе зададим в следующем виде

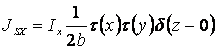,                         (12)

где   =1,   -b£y£b

Тогда, в итоге подставляя выражения (12) в (11) и в (1), получим соотношение для взаимной связи двух прямолинейных вибраторов на диэлектрической подложке с экраном

,

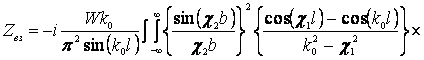
где W – сопротивление свободного пространства, Ф(c₁,c₂) определяется для разных значений d₁ :

1)  d₁=0

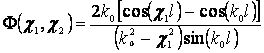   ,                                                 (14а)

2)  0<d₁<l,

     

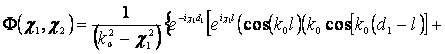
,              (14б)

3) d₁> l,

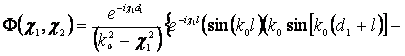
.          (14в)

Полученное выражение для взаимного сопротивления (14) представляет собой двойной интеграл Фурье по действительным переменным c₁ , c₂. Этот факт позволяет использовать алгоритм быстрого преобразования Фурье (БПФ), который в значительной степени сокращает время вычисления на ЭВМ.