Функция Грина для слоя диэлектрика на металле, страница 2

.

Подставляя последнее выражение в условия (1), (2), получаем граничные условия для функции А^м_х1, А^м_х :

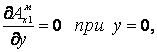                                     (6)

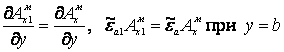.                   (7)

Уравнения (3), (4) совместно с граничными условиями (6), (7) составляют граничную задачу.

2.2.2. Решение граничной задачи

Для решения поставленной граничной задачи используем преобразование Фурье функций А^м_х1, А^м_х.

Сначала рассмотрим физические соображения, которыми руководствуются при решении задач. Сторонний ток возбуждает электромагнитное поле, которое, распространяясь в слое при 0£у£b, возбуждает поле и в верхнем полупространстве при у³b. Возбуждаемая вибратором волна, распространяясь в направлении границы у=0 под некоторым углом должна отразится. Отраженная волна, распространяясь в направлении верхней границы под некоторым углом, должна тоже частично или полностью отразится. Поле в слое диэлектрика образуется, таким образом, в результате наложения парциальных волн.

Полное электромагнитное поле Е₁, Н₁ в слое диэлектрика представим в виде суммы первичного поля Е^п₁, Н^п₁ и вторичного поля Е^в₁, Н^в₁. Первичное поле вычисляется в предположении, что сторонний источник расположен в неограниченном пространстве с параметрами . Вторичное поле обусловлено переотражениями от границ раздела или, другими словами, возникающими эквивалентными поверхностными токами на границах раздела сред. В соответствии с этими представлениями векторный потенциал А^м₁ полного поля тоже является суммой векторных потенциалов А^мп₁ первичного и А^мв₁ вторичного поля

.                                   (8)

Векторы А^мп₁, А^мв₁ удовлетворяют соответственно неоднородному и однородному уравнениям Гельмгольца. Граничные условия (6), (7) для А^мв₁ и (7) для А^м являются неоднородными, так как в них входит заданная функция А^мп₁. В математической записи неоднородности в граничных условиях можно считать источниками вторичных полей и, значит, функцией А^мв₁, А^м, удовлетворяющих однородному уравнению Гельмгольца.

Решение неоднородного уравнения (3) для А^мп_х1 определено формулой /(2.21) Петров/

.

Подставляя в эту формулу функцию Грина

,

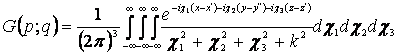и выражение тока

используя основное свойство d- функции

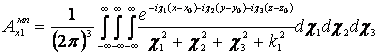
Выполняя интегрирование  по c₂ получаем

,

(9)

верхний знак берется при у-у₀<0, нижний – при у-у₀>0. Итак, магнитный векторный потенциал первичного поля при 0£у£b имеет только одну составляющую А^мп_х1. Магнитный векторный потенциал вторичного поля тоже имеет только одну составляющую А^мв_х1.

Поскольку вторичное поле Е^в₁, Н^в₁ обусловлено парциальными волнами, отраженными от границ раздела сред при у=0 и при у=b, представляем его в виде суммы полей, одно из которых обусловлено отражением от нижней границы раздела, а второе – от верхней. Решением однородного уравнения (3) для А^мв₁ тогда представляем  в виде суммы