Функция Грина для слоя диэлектрика на металле, страница 3

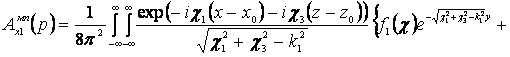
+,                                   (10)

где - спектральная плотность волн, возбуждаемых поверхностными токами, протекающими на металлической плоскости, при у=0; поскольку для этих волн у-b>0, то при показателе экспоненты взят знак “минус”. Аналогично - спектральная плотность волн, возбуждаемых эквивалентными поверхностными токами, протекающими на поверхности у=b; поскольку при этом у-b<0 , то при показателе экспоненты взят знак “плюс”. Из граничного условия (6) можно получить связь между функциями , . С учетом формул (8)-(10) из условия (6) получаем, используя обозначение    

.

Подставляя  в формулу (10), получаем

.                             (11)

Спектральную плотность  определим из граничного условия (7). Для этого надо записать разложение функции А^м_х. Поскольку в верхнем полупространстве сторонних источников нет, то поле Е, Н при у³b является вторичным. Составляющая векторного потенциала А^м_х этого поля определяются эквивалентными поверхностными токами (вторичными) при у=b. Поэтому решение уравнение (4) записываем в виде

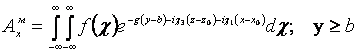,            (12)

где ,  - спектральная плотность; при показателе экспоненты взят знак “минус” с учетом условия излучения и расположения вторичных источников при у=b.

С развитием теории полосковых излучателей возникла необходимость определения  взаимной связи двух печатных вибраторов. В работах /5/ и /3/ производится анализ взаимной связи между бесконечными полосковыми излучателями и конечными полосковыми вибраторами. В данной работе представлены выражения для взаимной связи, используя тензорную функцию Грина, и результаты расчета взаимного сопротивления. Строгая электродинамическая постановка вопроса дает возможность исследовать взаимную связь при наличии поперечной электрической (ТЕ) и поперечной магнитной (ТМ) волн /4/ (ТМ волна частоты среза не имеет). Толщина подложки и относительная диэлектрическая проницаемость определяют число поверхностных волн, которые могут поддерживаться подложкой для данной частоты /2/. Это в основном и определяет взаимную связь между двумя полосковыми излучателями, которую можно определить, используя общее выражение для взаимного сопротивления

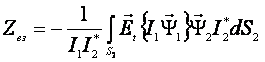,                   (1)

где - линейный оператор, позволяющий вычислить тангенциальное поле, возбуждаемое первым излучателем на поверхности второго

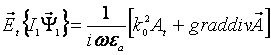 .                            (2)

Векторный потенциал для произвольного распределения сторонних токов в объеме V может быть представлен через тензор Грина G в виде /1/

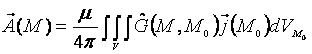,                       (3)

где ,

      - тензорная функция источника, имеющая вид

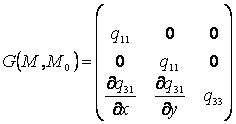                              (4)