 (7.1)
(7.1)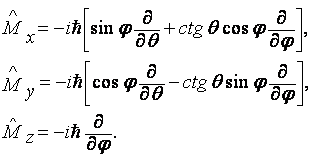
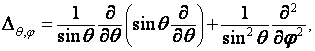 поэтому
уравнение (7.2) принимает вид:
поэтому
уравнение (7.2) принимает вид: 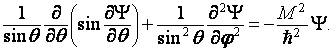
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
обозн. |
s |
p |
d |
f |
g |
h |
i |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.