МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТАГАНРОГСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
По дисциплине «Высшая математика»
«Метод LU разложения и метод Холесского для решения СЛАУ»
Выполнил: студент гр. Р-74
Емельяненко
ВАРИАНТ №1
Теоретическое введение:
Данный алгоритм можно рассматривать как конкретную форму метода Гаусса. Алгоритм LU-разложения используется не только для решения СЛАУ, но и также для обращения матрицы, т.е. вычисления матрицы, обратной данной.
Пусть  и A=LU (2.1),
и A=LU (2.1),
где L и U – соответственно нижняя и верхняя треугольные матрицы вида
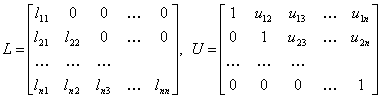 .
.
Известно, что если все угловые миноры матрицы А отличны от нуля, т.е.
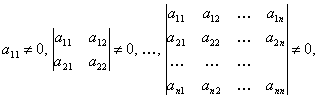
то разложение вида (2.1) существует и единственно, однако, на доказательстве этого факта мы останавливаться не будем. Для того чтобы получить расчётные формулы, поступим следующим образом. Обозначим aij как произведение i-ой строки матрицы L на j-ый столбец матрицы R, причём будем считать в начале , что i<j.
Тогда ![]() .
.
Выразим из последней формулы uij.
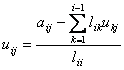 . (2.2)
. (2.2)
Как это принято, будем считать в
формуле (2.2) и далее, что сумма вида ![]() равна нулю, если значение верхней границы
индекса суммирования меньше нижней границы.
равна нулю, если значение верхней границы
индекса суммирования меньше нижней границы.
В случае i = j имеем
![]()
Учитывая, что uii º 1 и, выражая из последнего соотношения lii, получаем:
![]() (2.3)
(2.3)
Наконец, при i > j получаем
![]()
откуда, с учетом того, что ujj º 1 приходим к формуле
![]() (2.4)
(2.4)
Итак, расчетные формулы (2.2) – (2.4) получены. Для того чтобы при их применении не использовались неизвестные (не вычисленные) величины, необходимо выбрать соответствующий порядок вычисления элементов матриц L и U.
Например, можно рекомендовать порядок расчета элементов матриц L и U, схематически изображенный на рис.1. На нем цифры слева для матрицы L и сверху - для матрицы U означают, что на первом шаге рассчитывается l11 по формуле (2.3), затем вычисляется элемент u12 по формуле (2.2).
Далее (3 шаг) определяются элементы второй строки матрицы L в порядке, указанном стрелкой: l21 и l22 (по формулам (2.4) и (2.3) соответственно).
На 4 шаге выполняется расчет элементов 3 столбца матрицы U в порядке, обозначенном стрелкой: u13, u23 (формулы (2.2)) и т.д.

Рис.1.
Пример 1. LU – разложение матрицы.

По формуле (2.3) для i = 1 определяем l11 = а11 = 2. В соответствии с рис. далее вычисляем u12 по формуле (2.2)
![]()
Переходим к определению элементов второй строки матрицы L (см. рис.1) по формулам (2.4) и (2.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.