Метод LU разложения и метод Холесского для решения СЛАУ, страница 2

l21 = а21 = 1, l22 = а22 -

Следующий этап – расчет элементов третьего столбца матрицы U по формуле (2.2)

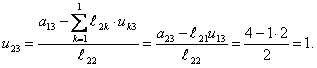
Завершающий этап – определение элементов 3 строки матрицы L

l31 = a31 = 1; l32 = a32-

l33 = a33 -

Выпишем полученное разложение, учитывая, что по определению u11 = u22 = u33 = 1

Рассмотрим теперь применение LU-разложения для решения СЛАУ вида

Ах = f,

где

A = LU.

Введем вспомогательный вектор у,

у = U × x.                                                            (2.5)

Тогда исходную систему можно записать так

L × Ux = b ó Ly = b.                                                     (2.6)

В силу формул (2.5) и (2.6) решение исходной СЛАУ сводится к последовательному решению систем (2.6) и (2.5) соответственно с верхней и нижней треугольной матрицами.

Пример 2. Используя метод LU-разложения решить СЛАУ вида

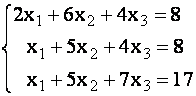
Заметим, что матрица данной системы совпадает с матрицей А из примера 1, для которой требуемое разложение уже получено. Таким образом, решение данной системы сводится к последовательному решению систем

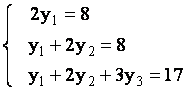            и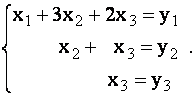         

Из первой системы последовательно находим

у1 = 8 / 2 = 4

2у2 = 8 – у1 = 8 – 4 = 4 => y2 = 4 / 2 = 2

3y3 = 17 – y1 – 2y2 = 17 – 4 – 2 × 2 = 9 => y3 = 3.

Подставляя найденные значения у1, у2 и у3 во вторую систему, и последовательно определяем х3, х2, х1:

х3 = у3 = 3;

х2 = у2 – х3 = 2 – 3 = -1;

х1 = у1 – 3х2 – 2х3 = 4 – 3 (-1) – 2 × 3 = 1.

Непосредственной подстановкой найденных значений х1, х2 и х3 в исходную систему можно убедиться, что решения найдены верно.

2.2. Алгоритм треугольного разложения положительно определенных симметричных матриц и его применение для решения СЛАУ.

Этот алгоритм называют еще алгоритмом Холесского разложения матриц. Он применим к симметричным положительно определенным матрицам.

Напомним, что матрица А = (аij)ni,j=1 называется симметричной, если A = AT, где

АТ = (аji)ni,j=1.

Матрица А называется положительно определенной, если скалярное произведение (Ах, х) > 0 для всех ненулевых векторов, или что то же самое хТ×Ах > 0. Такие матрицы часто встречаются в приложениях. В типичной ситуации произведение хТ×Ах представляет собой энергию некоторой физической системы, которая положительна для любого вектора х состояния системы.

Приведем для справки два критерия положительной определенности матрицы.

1.  Критерий Сильвестра. Для того чтобы симметричная матрица А=(аij)ni,j=1 была положительно определенной, необходимо и достаточно чтобы все ведущие (угловые) миноры этой матрицы были положительными, т.е.

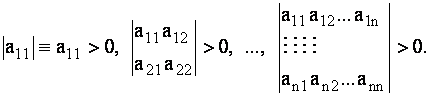
2.  Для того, чтобы матрица А = (аij) была положительно определенной, достаточно, чтобы аii>0, i=1,2,...,n; и для всех строк матрицы А выполнялось свойство диагонального преобладания:

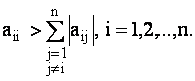
Кроме того, известно, что у положительно определенной матрицы и только у нее все собственные значения положительны.

Теорема (о разложении Холесского). Если А=(аij)ni,j=1 симметричная положительно определенная матрица, то существует и единственно ее треугольное разложение вида

А = L × LT, где L - нижняя треугольная матрица вида