Метод LU разложения и метод Холесского для решения СЛАУ, страница 3

,              lii > 0,             i = 1, 2, ..., n,

a LT - транспонированная по отношению к L матрица вида

.

На основе этой теоремы может быть построен алгоритм вычисления разложения, который мы приводим без вывода (так называемый алгоритм в форме скалярных произведений).

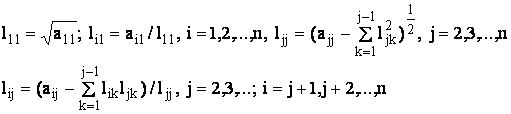
Элементы матрицы L рассчитывают в следующем порядке: l11, l21, l22, l31, l32, l33, l41, l42, l43, l44 и т.д., выбирая одну из формул, приведенных выше.

Цель работы:  

Освоить Метод LU разложения и метод Холесского для решения СЛАУ, используя программный пакет Mathcad 2000 Professional.

Задание:

Вывод:

Изучили Метод LU разложения и метод Холесского для решения СЛАУ . На практике, используя программный пакет Mathcad 2000 Professional для решения математических задач, изучили данный метод. Результаты, полученные программой совпадают с результатами полученными практически.