нахождения условного максимума :
лежит среди стационарных точек функции ЛагранжаП
лежит среди точек максимума функции Лагранжа
лежит среди точек минимума функции Лагранжа
совпадает с точками максимума функции Лагранжа
точкой минимума функции Лагранжа
точкой максимума функции Лагранжа
седловой точкой функции Лагранжа
стационарной седловой точкой функции ЛагранжаП
Lj-1=Lj+Lj+1 П
Lj+1=Lj+Lj-1
Lj=Lj-1+Lj+1
Lj=Lj-1-Lj+1
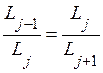 =...=2
=...=2
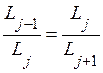 =...=
=...=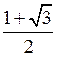
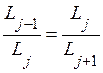 =...=
=...=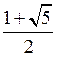 П
П
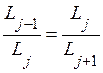 =...=
=...=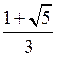
вектор нормали к линии уровня
касательный вектор к линии уровня
вектор градиента функции f
вектор вида (0, 0, …,0, 1, 0, …0)П
х1 + х2
х1 - х2П
1+ х1х2
1- х1х2
вектор нормали к линии уровня функции f(x) в данной точке
касательный вектор к линии уровня функции f(x) в данной точке
вектор градиента функции f(x) в данной точке П
единичные координатные векторы
не требует вычисления производных минимизируемой функции
требует вычисления всех первых производных минимизируемой функции П
требует вычисления некоторых первых производных минимизируемой функции
требует вычисления вторых производных минимизируемой функции
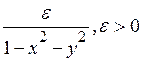 П
П
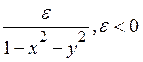
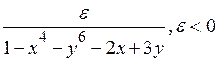
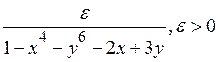
2х+3у®max
х+у£10, х³ 0, у³0
не имеет решения
имеет решение (0,10)П
имеет решение (10, 0)
имеет решение (5. 5)
ограниченное множество
всегда неограниченное множество
невыпуклый многогранник
выпуклый многогранник, возможно пустой или неограниченный П
Итоговый тест
Итоговый тест включает в себя вопросы контрольного теста №1 и следующие вопросы
модули вариации d(у) = у1(х) - у(х) и всех ее производных до порядка k включительно малыП
модули вариации d(у) = у1(х) - у(х) и всех ее производных до порядка k малы
модули всех производных порядка k включительно вариации d(у) = у1(х) - у(х) малы
модули вариации d(у) = у1(х) - у(х) и всех ее производных порядка выше k малы
близки в смысле нулевого порядка для любого nП
близки в смысле первого порядка для любого n
близки в смысле бесконечного порядка для любого n
не являются близкими ни в каком смысле
J[y(x)] = 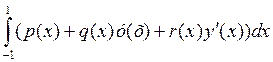
является непрерывным в смысле близости 1-го порядка
при любой функции у(х) Î С1[-1, 1] и произвольных функциях p, q и r
при любой функции у(х) Î С1[-1, 1] и интегрируемых на [-1, 1] функциях p, q и r П
при любой функции у(х) и произвольных функциях p, q и r
при любой функции у(х) и дифференцируемых функциях p, q и r
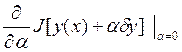 П
П
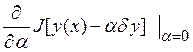
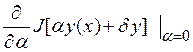
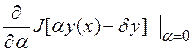
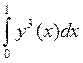 равна
равнаdJ[y(x)] = 3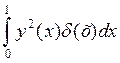 П
П
dJ[y(x)] = 3у2(х)
dJ[y(x)] = 3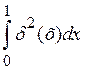
dJ[y(x)] = 3d2(х)
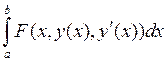 имеет
вид
имеет
вид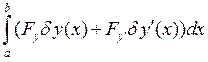 =0
=0
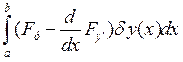
![]() =0
=0
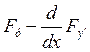 =0П
=0П
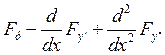 =0
=0
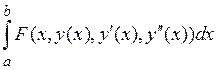 имеет
вид
имеет
вид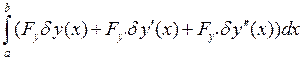 =0
=0
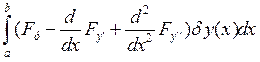
![]() =0
=0
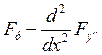 =0
=0
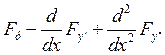 =0П
=0П
F-y¢Fy¢½x=x0=0, Fy¢½x=x0=0П
F+y¢Fy¢½x=x0=0, Fy¢½x=x0=0
F-y¢Fy¢½x=x0=0, Fy½x=x0=0
Fу-y¢Fy¢½x=x0=0, Fy¢½x=x0=0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.