6. F(x, y) = 10x4+xy+y6- 12exp(-x2-y2) в области 0£(х, у)£1.
7. F(x, y) = 3x4+y6- exp(-x2-y2)–y+2 в симплексе х ³0, у ³0, х+у £1.
8. F(x, y) = 4x4+4x+y6- exp(-x2-3y2) в
области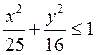 
9. F(x, y) = 5x4+4y+ exp(-x2-y2)-2x2 внутри области:
у³0, у£1-х2.
10. F(x, y) = 7x4+16y6-2x2 - exp(-4x2-y2) внутри области:
у³-2, у£1-4х2.
11. F(x, y) = 10x4+16y6- exp(-4x2-y2) в области 0£(х, у)£4.
12. F(x, y) = x4+8xy+y6- 12exp(-x2-y2) в области 0£(х, у)£15.
13. F(x, y) = x4+y6- exp(-x2-y2)–y+2 в симплексе х ³0, у ³0, х+у £16.
14. F(x, y) = 3x4-4y6- exp(-2x2-y2)–y+2 в треугольнике
х ³-2, у ³-3, х+у £1.
15. F(x, y) = x4+(x-2y)2+y6- exp(-3x2-y2) внутри области 2х2+4у4£32.
16. F(x, y) = x4+6x2y4+4y6-12x2 –y в круге 2х2+3у2£36.
17. F(x, y) = x4+4xy+y6-exp(-x2-y2) в области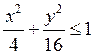 
.
18. F(x, y) = 4x4+4x+y6- exp(-x2-3y2) в области симплексе
х ³0, у ³0, х+у £16.
19. F(x, y) = x4+8xy+y6- 12exp(-x2-y2) в области
у³-2, у£1-4х2.
20. F(x, y) = x4+4xy+y6-7exp(-x2-y2) в области 2х2+4у4£16.
21. F(x, y) = 5x4+(x-2y)2+y6- exp(-3x2-2y2) внутри области
х ³-5, у ³-10, х+у £10.
22. 2x4+7y6-2x2 -25 exp(-4x2-y2)
внутри области: .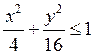
23. F(x, y) = 5x4+(x-2y)2+y8-
exp(-3x2-2y4) внутри эллипса .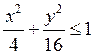
24. F(x, y) = 8x4+4xy+y6-2x2
–
в области
у³-2, у£1-4х2.
25. F(x, y) = 8x4+
+4xy+y6 в единичном круге с центром в точке (-2, 3).
Виды и формы деятельности студентов определяются по согласованию с деканатом.
Расчетно-графическое задание выполняется в тетради или на листах формата А4. Работа начинается с титульного листа, оформленного по следующей схеме:
наименование вуза
наименование кафедры
название
работы
кто выполнил кто проверил
студент группы.... ...должность
ФИО ФИО
место нахождения вуза
год
Численные расчеты производятся с применением любого, известного студенту, математического пакета (Excel, Maple, Matlab и т.д.) или ручную. Распечатки или результаты расчетов должны быть приведены.
Номер задания выбирается в соответствии с номером записи фамилии студента в учетной ведомости деканата.
Расчетно-графическое задание должно быть сдано для проверки не позднее 16 недели семестра.
Вопросы контрольного теста № 1
имеет одну точку локального минимумаП
имеет две точки локального минимума
имеет три точки локального минимума
не имеет точек локального минимума
имеет одну точку глобального минимума
имеет две точки глобального минимума
имеет три точки глобального минимума
не имеет точек глобального минимумаП
имеет одну точку локального максимумаП
имеет две точки локального максимума
имеет три точки локального максимума
не имеет точек локального максимума
имеет одну точку глобального максимума
имеет две точки глобального максимума
имеет три точки глобального максимума
не имеет точек глобального максимумаП
минимума
всегдаП
никогда
только для выпуклых функций
только для функций одного переменного
всегда
никогдаП
только для выпуклых функций
только для функций одного переменного
=0
grad f(x)=0П
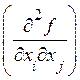³0
>0 для всех i.
grad f(x)=0
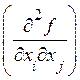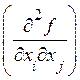grad f(x)=0 и ³0
³0
grad f(x)=0 и 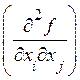£0П
f(x1, x2,…,xn)®max
g1 (x1, x2,…,xn)=0
g2 (x1, x2,…,xn)=0
……………..
gm (x1, x2,…,xn)=0
имеет вид:
f(x1, x2,…,xn)+
П
f(x1, x2,…,xn)+
f(x1, x2,…,xn)-
f(x1, x2,…,xn)+
g1 (x1, x2,…,xn)=0
g2 (x1, x2,…,xn)=0
……………..
gm (x1, x2,…,xn)=0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.