|
А) |
№№ 16.137-16.143 нечетные из [1]. |
|
С) |
№№ 16.136-16.144 четные из [1]. |
Раздел 2.
Занятие 2.1 Вариация функции и ее свойства.
|
А) |
№№ 46-58 из [3]. |
|
С) |
№№ 16.376-16.386 четные из [1]. |
Занятие 2.2 Уравнения Эйлера..
|
А) |
№№ 71-80 из [3]. |
|
С) |
№№ 16.388-16.398 из [1]. |
Занятие 2.3 Уравнения Эйлера..
|
А) |
№№ 81-90 из [3]. |
|
С) |
№№ 16.401-16.411 нечетные из [1]. |
Занятие 2.4 Условия трансверсальности.
|
А) |
№№ 172-180 из [3]. |
|
С) |
№№ 16.421-16.427 нечетные из [1]. |
Занятие 2.5 Достаточные условия. Признаки Вейерштрасса и Лежандра..
|
А) |
№№ 135, 143, 146, 148, 156, 164 из [3]. |
|
С) |
№№ 142, 154, 165 из [3]. |
Лабораторные работы учебным планом на предусмотрены.
График контроля самостоятельной работы студентов устанавливается по согласованию с деканатом.
Задание 1 Найти точки экстремума и установить его характер. Затем проверить найденное решение методами покоординатного и градиентного спусков. Провести сравнительный анализ методов.
1. F(x, y, z) = 3x2+2xz+12y2+3yz+4z2-2x-3y-4z.
2. F(x, y, z) = 2x2+3xz+13y2+4yz+3z2-4x-5y-5z.
3. F(x, y, z) = 4x2+4xz+10y2-3yz+2z2-6x-7y-6z.
4. F(x, y, z) = 5x2+5xz+12y2+5yz+10z2-7x-9y-7z.
5. F(x, y, z) = 6x2+6xz+13y2+3yz+13z2-2x-3y-9z.
6. F(x, y, z) = 8x2+7xz+14y2+36z+15z2-x-y-5z.
7. F(x, y, z) = x2+21xz+19y2+7yz+14z2-3x-3y-4z.
8. F(x, y, z) = 12x2-8xz+y2+3yz+17z2-2x-12y-8z.
9. F(x, y, z) = 31x2+9xz+16y2+8yz+4z2-5x-15y-4z.
10. F(x, y, z) = 2x2+2xz+15y2+3yz+3z2-7x-3y-12z.
11. F(x, y, z) = 4x2+2xz+16y2+9yz+23z2-2x-4y-14z.
12. F(x, y, z) = 5x2+2xz+12y2+10yz+24z2-4x-3y-3z.
13. F(x, y, z) = 6x2+2xz+21y2+11yz+4z2-2x-21y-9z.
14. F(x, y, z) = 7x2+2xz+14y2+3yz+4z2-7x-y-8z.
15. F(x, y, z) = 8x2+2xz+15y2+12yz+4z2-12x-7y-9z.
16. F(x, y, z) = 9x2+2xz+16y2+3yz+14z2-2x-3y-4z.
17. F(x, y, z) = 2x2+3xz+17y2+13yz+4z2-12x-6y-6z.
18. F(x, y, z) = 3x2+4xz+58y2+4yz+14z2-21x-3y-4z.
19. F(x, y, z) = 21x2+4xz+9y2+15yz+24z2-22x-5y-14z.
20. F(x, y, z) = 32x2+2xz+10y2+3yz+14z2-25x-4y-4z.
21. F(x, y, z) = 341x2+2xz+11y2+16yz+24z2-27x-3y-4z.
22. F(x, y, z) = 31x2+5xz+y2+12yz+16z2-12x-y-4z.
23. F(x, y, z) = 124x2+3xz+y2+3yz+17z2-12x-3y-21z.
24. F(x, y, z) = 54x2+7xz+12y2+4yz+24z2-6x-3y-z.
25. F(x, y, z) = 27x2+9xz+33y2+5yz+44z2-7x-y-4z.
Задание 2. Методом покоординатного спуска найти точку минимума с погрешностью e = 0,001.
1. F(x, y) = x4+4xy+y6-2x2 –y+![]()
2. F(x, y) = x4+x2y4+4y6-12x2 –y
3. F(x, y) = 8x4+xy2+y6-2x –y+12
4. F(x, y) = x4+xy+y6-exp(-x2-y2)
5. F(x, y) = x4+(x-2y)2+y6- exp(-3x2-y2)
6. F(x, y) = 10x4+xy+y6- 12exp(-x2-y2)
7. F(x, y) = 3x4+y6- exp(-x2-y2)–y+2
8. F(x, y) = 4x4+4x+y6- exp(-x2-3y2)
9. F(x, y) = 5x4+4y+ exp(-x2-y2)-2x2
10. F(x, y) = 7x4+16y6-2x2 - exp(-4x2-y2)
11. F(x, y) = 8x4+4xy+y6-2x2
–![]()
12. F(x, y) = 13x4+![]() +y6-2x2 –y+2
+y6-2x2 –y+2
13. F(x, y) = 11x4+4xy+y6-![]() +22
+22
14. F(x, y) = 21x4+4xy+![]() -2x2 –y+12
-2x2 –y+12
15. F(x, y) =15 x4+![]() +y6-2x2 –y+32
+y6-2x2 –y+32
16. F(x, y) = 41x4+![]() –y+12
–y+12
17. F(x, y) = 6x4+4xy+y6-![]() +12
+12
18. F(x, y) = ![]() +4xy+y6-2x2
–y+12
+4xy+y6-2x2
–y+12
19. F(x, y) = 22x4+4xy+y6-![]() +12
+12
20. F(x, y) = 9x4+xy+y6-2x2
–![]()
21. F(x, y) = 8x4+![]() +4xy+y6
+4xy+y6
22. F(x, y) = 7x4+![]() +y6-2x2
+y6-2x2
23. F(x, y) = ![]() +4xy+
+4xy+![]()
24. F(x, y) = ![]() +y6-2x2
–y+12
+y6-2x2
–y+12
25. F(x, y) = 4x4+![]() +
+![]()
Задание 3. Методом штрафных функций найти наибольшее значение функции в области с погрешностью e = 0 .005. Для реализации метода применить метод покоординатного спуска.
1. F(x, y) = x4+x2y4+4y6-12x2 –y в круге х2+у2£6.
2. F(x, y) = x4+x2y4+4y6-12x2 –y в единичном круге с центром в точке (2, 3).
3. F(x, y) = 8x4+4xy2+y6-2x –y+12 в круге с центром в точке (1, -1) радиуса 7.
4. F(x, y) = x4+4xy+y6-exp(-x2-y2) в области 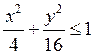 .
.
5. F(x, y) = x4+(x-2y)2+y6- exp(-3x2-y2)
в области 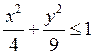 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.