8. Как осуществляется морфологическое выделение контуров и углов?
9. Как вычисляется морфологический спектр? Какие особенности формы изображений он отражает?
10. Как определяется морфологический скелет бинарной фигуры?
11. Для чего в дискретном случае применяется процедура утончения?
12. Как вычисляется непрерывный скелет многоугольной фигуры? Отрезки каких кривых в него входят?
13. Как формируется и используется непрерывное гранично-скелетное представление бинарных изображений?
14. Почему задача вычисления скелета является некорректной? Как производится регуляризация скелетов?
15. Чем операторы селективной морфологии отличаются от операторов классической ММ?
К разделу 6.2:
16. Какова математическая модель «формы» изображений по Пытьеву?
17. Как вычисляется проекция изображения на форму другого изображения?
18. Как вычисляется морфологический коэффициент корреляции по Пытьеву? Почему в общем случае он не симметричен K(f,g)¹K(g,f)?
19. Что означает отношение «более сложный по форме»? Это отношение частичного или полного порядка? Какие изображения считаются сравнимыми по форме?
20. Как в морфологии Пытьева решается задача выделения отличий изображений по форме?
21. Как в морфологии Пытьева решается задача обнаружение объекта по его изображению и оценки его координат?
22. Задача: заданы два кусочно-постоянных изображения f и g. Найти проекцию f на g и g на f. Сравнимы ли эти фигуры по форме? Чему равен морфологический коэффициент корреляции K(f,g)?
а) 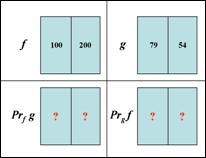 б)
б) 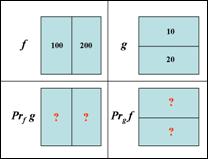
в) 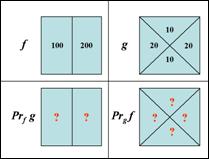 г)
г) 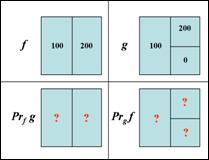
д) 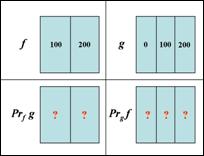
23. Задача: заданы два кусочно-постоянных изображения f и g. Найти форму FÙG, которая не проще одновременно формы F и формы G. Найти форму FÚG, которая не сложнее одновременно формы F и формы G.
а) 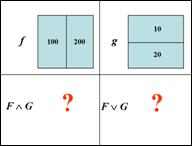 б)
б) 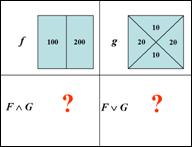
в) 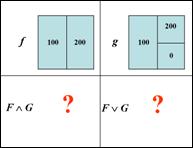
24. Как вычисляется проекция на форму в морфологии на базе кусочно-линейной интерполяции? Какие элементы изображения характеризуют форму? Как вычисляется здесь морфологический коэффициент корреляции?
К разделу 3.2:
Задача 13. Пусть на изображении имеется одна связная область яркости 1, окруженная фоном яркости 0. Площадь ее составляет 110 пикселей, а габаритные размеры – 12´13 пикселей. Каковы должны быть минимальные размеры квадратного окна фильтрации, чтобы медианный фильтр целиком удалил эту область с изображения.
Ответ: Минимальная площадь окна фильтрации медианой, целиком удаляющей область плошадью 110 пикселей будет (2´110+1) = 221. Ближайший больший квадрат целого числа это 15´15 = 225 > 221. Значит, медианный фильтр с окном размера 15´15 гарантированно удалит все пиксели данной области с изображения.
Задача 14. Пусть на изображении имеется одна связная область яркости 0, окруженная фоном яркости 1. Область представляет собой квадрат 11´11 пикселей. Нарисуйте (схематично) как будут выглядеть результаты фильтрации этого изображения медианным фильтром с размером окна 11´11 пикселей.
Ответ: Площадь окна фильтрации 11´11=121, следовательно, для того, чтобы выход фильтра был равен 0, в апертуре должно наблюдаться не менее [121/2]+1=61 пикселя со значением 0. Ниже приведен квадрат 11´11 пикселей, и в каждом пикселе указано число единиц в апертуре 11´11 вокруг данного пикселя. Легко увидеть, что это фрагмент школьной таблицы умножения. Серым помечены пиксели, которые имеют менее 61 нулевого соседа, и следовательно будут заменены на 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.