Задание для студентов на практическое №3 по теме
«Основы интегрального исчисления. Методы нахождения неопределенных интегралов. Вычисление определенных интегралов»
Цель занятия: Научиться решать примеры и задачи по данной теме
Вопросы теории ( исходный уровень)
1. Первообразная функции и неопределённый интеграл.
2. Интегрирование.
3. Методы нахождения неопределенных интегралов: приведение к табличному виду и метод замены переменной, интегрирование по частям.
4. Определённый интеграл, его применение для вычисления площадей фигур и работы переменной силы.
5. Вычисление определенных интегралов, правило Ньютона-Лейбница.
6. Примеры использования интегрального исчисления в медицинских задачах. (самостоятельная подготовка)
Содержание занятия:
1.ответить на вопросы по теме занятия
2.решить примеры
Примеры
Найти интегралы:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
11)
|
12)
|
|
13)
|
14)
|
15)
|
|
16)
|
17)
|
18)
|
|
19)
|
20)
|
21) |
|
22) |
23) |
24) |
|
25) |
26) |
27) |
Вычислить интегралы:
|
1) |
2) |
3) |
|
4) |
5) |
6) |
|
7) |
8) |
9) |
|
10) |
11) |
12) |
|
13) |
14) |
15) |
|
16) |
17) |
18) |
|
19) |
21) |
22) |
|
23) |
24) |
25) |
|
26) |
27) |
28) |
|
29) |
30) |
31) |
|
32) |
33) |
34) |
|
35) |
36) |
37) |
|
38) |
Тема
Неопределенный интеграл
Функция F(x), имеющая данную функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции f(x). Совокупность всех первообразных функций для дифференциала f(x)dx называется неопределенным интегралом и обозначается символом ∫ f(x)dx.
Свойства неопределенного интеграла
∫f(x)dx=F(x)+C
∫[f(x)+φ(x)]dx=∫ f(x)dx+∫φ(x)dx
∫ d(F(x))=F(x)+C
(∫f(x)dx)=f(x)
∫f(x)dx= ∫f(t)dt
d∫f(x)dx=f(x)dx
∫af(x)dx+a∫f(x)dx
Основные интегралы
∫dx=x+C
∫xndx=xn+1/ (n+1) +C (n≠-1)
∫dx/x=ln|x|+C
∫axdx=ax/lna +C
∫exdx=ex+C
∫sin x dx=-cos x +C
∫cos xdx=sin x +C
∫dx/cos2x=tgx+C
∫dx/sin2x=-ctgx+C
∫dx/(1-x2)1/2=arcsinx=-arccosx
∫dx/(1+x2)= arctgx=- arcctgx
Интегрирование по частям
∫ udv = uv—∫ vdu.
Пример
Найти у = ∫ ln хdх.
Полагаем и=lпх, dv = dx, тогда dи =dx/x, v = x
Используя формулу интегрирования по частям, получаем
у = ∫ ln xdx = x ln х-∫ dх = xlnx-x+C
Пример метод непосредственного интегрирования
Найти у= ∫ (1+ 2x2)dx
На основании свойства интеграла суммы запишим
у= ∫ (1+ 2x2)dx = ∫ dx+2 ∫ x2dx =x+2x3/3+C
Пример; метод замены переменной( метод подстановки)
∫tgxdx=∫(sinx/cosx)dx обозначим cosx=t
Продифферинцируем праву и левую часть
-sinxdx=dt найдем dx=dt/(-sinx)
Запишим интеграл через новые переменные
∫(sinx/t) dt/(-sinx) =-∫dt/t= lnt+C или lncosx+C
Определенный интеграл
Определенный интеграл функции f(x) на отрезке [а, b] представляет предел интегральной суммы
lim∑f(ki)Δxi ( от i=1 до n и Δx→0)
где ki — произвольная точка соответствующего отрезка.
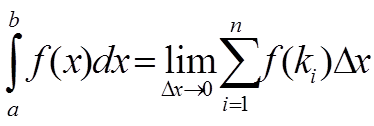
Формула Ньютона — Лейбница
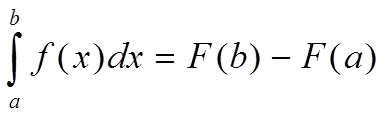
где F′ — первообразная функцию f(x), т е
F′(x)=f(x)
Некоторые свойства определенного интеграла
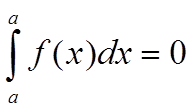
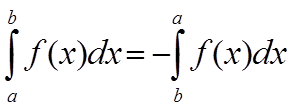
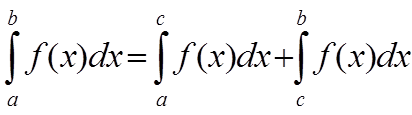
Площадь криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х=а и х=b,
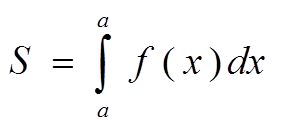
Площадь фигуры, ограниченной двумя кривыми y=.f1(x) и у = = f2(x) [ f'2(x)≥f1(x)] и двумя прямыми х=а и х=b,
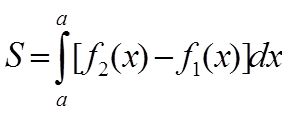
Дифференциальные уравнения
Общий вид дифференциального уравнения
F(x ,y,y′,y″,…yn) = О
Общee решение дифференциального уравнения
y=f(x, C1,C2, , Сn)
Общий вид дифференциального уравнения первого порядка
F(x,y,y') = 0
Общее решение дифференциального уравнения первого порядка
y= f(x,C)
примеры
1 Дифференциальное уравнение типа y'=f(x)
dy/dx=f(х) , dx = f(x)dx
Общее решение
y=∫f(x)dx=F(x)+C
Дифференциальное уравнение типа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.