Это свойство доказывается также с помощью дифференцирования.
ОСНОВНЫЕ ФОРМУЛЫ ИНТЕГРИРОВАНИЯ.
Приведем формулы, которые можно проверить дифференцированием.
1. ò dx = x + C.
2.
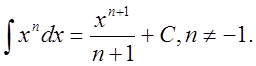
3.
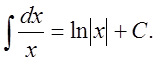
4. ò axdx = ax/ln a + C.
5. ò exdx = ex + C.
6. ò cosxdx = sin x + C.
7. òsin xdx = - cos x + C.
8.
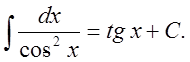
9.
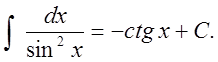
10.
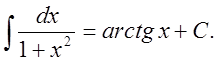
11.
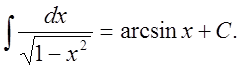
12. ò tg xdx = - ln |cos x| + C.
13. ò ctg xdx = ln |sin x| + C.
14.
![]()
15.
![]()
16.
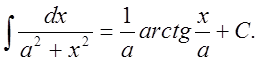
17.
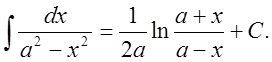
18.
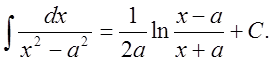
19.
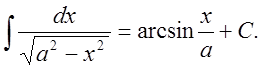
20.
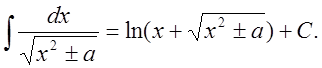
21.
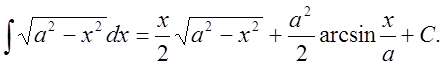
22.
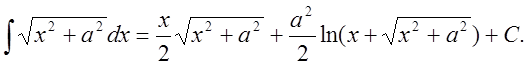
23.
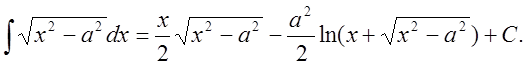
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
ПРОСТЕЙШИЕ СПОСОБЫ ИНТЕГРИРОВАНИЯ.
Непосредственное интегрирование. Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме.
Пример. Вычислить ò(2х3 – 3x2 + 2х –7)dx.
Решение. В данном примере под знаком интеграла стоит алгебраическая сумма функций. Согласно свойству 5 неопределенного интеграла.
ò(2х3 – 3х2 +2х –7)dx = ò2x3dx - ò3x2dx + ò2xdx - ò7dx.
Последовательно применяя свойство 4 интегралов и формулы 1 и 2, получаем
ò(2х3 – 3х2 + 2х – 7)dx = 2òx3dx -3òx2dx + 2òxdx - 7òdx=
=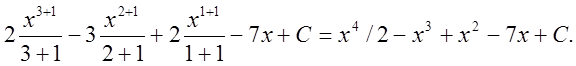
Интегрирование подстановкой (заменой переменной). Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.
В интеграле ò f(x)dx сделаем подстановку x = j(t), гдеj(t) – функция, имеющая непрерывную производную. Тогда:
f(x) = f(j(t)); dx = j¢(t)dt; òf(x)dx = ò f(j(t))j¢(t)dt.
Пример. Вычислить ò sin7xcosxdx.
Решение. Вычислим интеграл, использовав метод подстановки:
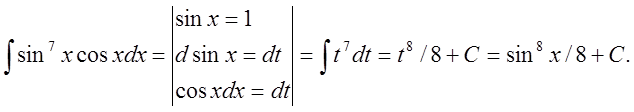
Интегрирование по частям. Если и = и(х) и ![]() - дифференцируемые функции, то
- дифференцируемые функции, то ![]() откуда
откуда ![]() Интегрируя
последнее выражение, получаем
Интегрируя
последнее выражение, получаем
![]()
или
![]() (1)
(1)
Это и есть формула интегрирования по частям.
Способ интегрирования по частям применяется в том случае, когда интеграл в правой части формулы (1) более прост для вычисления, чем исходный.
Пример. Вычислить ò xlnxdx.
Решение. Обозначим lnxчерез и тогда xdx = du. Находим:
du = d(lnx) = 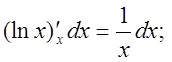 ò du = òxdx;
ò du = òxdx; 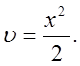
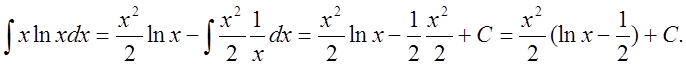
В некоторых случаях для сведения данного интеграла к табличному формула (1) применяется несколько раз.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Рассмотрим свойства определенного интеграла.
1. Определенный интеграл не зависит от обозначения переменной интегрирования, то есть
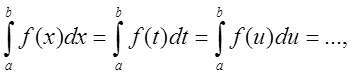
так как интегральные суммы представляют собой числа.
2. Определенный интеграл от суммы конечного числа непрерывных функций f1(x), f2(x), …, fn(x), заданных на отрезке [а, в], равен сумме определенных интегралов от слагаемых функций:
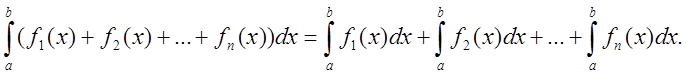
3. Постоянный множитель r подынтегральной функции можно выносить за знак определенного интеграла:
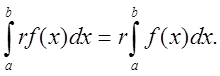
4. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл сохранит абсолютную величину и изменит свой знак на противоположный:
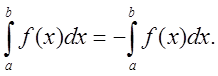
Если пределы интегрирования равны между собой (b=а), то определенный интеграл равен нулю:
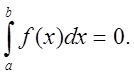
5. Если существуют интегралы 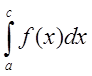 и
и 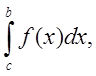 то существует
также
то существует
также 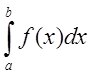 и для любого взаимного расположения
точек а, в, с
и для любого взаимного расположения
точек а, в, с
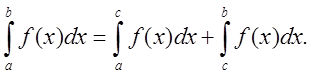
6.
Если подынтегральная функция на отрезке интегрирования сохраняет постоянный
знак, то интеграл представляет собой число того же знака, что и функция, то
есть если ![]() то
и
то
и 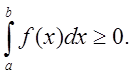
10. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА:
Найдите интегралы:
1. ![]() 2.
2.
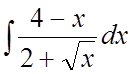 3.
3. ![]() 4.
4.
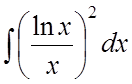 5.
5. 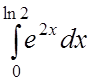
ЛИТЕРАТУРА
1. Лобоцкая Н.Л. Основы высшей математики - М.: «Вышэйшая школа», 1978.C198-226.
2. Бейли Н. Математика в биологии и медицине. Пер. с англ. М.: «Мир», 1970.
3. Ремизов А.Н., Исакова Н.Х., Максина Л.Г. Сборник задач по медицинской и биологической физике – М.: «Высшая школа», 1987. С16-20.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.