Анализ системы, определение динамических и статических показателей качества системы

Задание к работе и исходные данные.

Произвести анализ предложенной системы, определить динамические и статические показатели качества системы. Выполнить моделирование системы на ЭВМ. Затем разработать корректирующее звено и проверить работу скорректированной системы. При этом система должна остаться того же типа, что и исходная (статическая или астатическая). Требования к системе:

1. Статическая ошибка не должна превышать 5%

2. Длительность переходного процесса должна быть на порядок меньше, чем в исходной системе.

3. Перерегулирование при отработке единичного ступенчатого сигнала не должно превышать 5% от установившегося значения управляемой величины.

Уравнения системы:

y₁ = y

x₁ = (y₂ + y₄) - z

x₂ = x₄ = y₃

x₃ = x - y

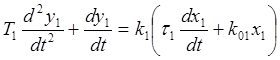
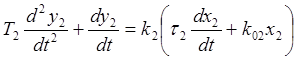
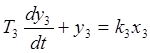
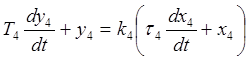
Значение коэффициентов k, k₀, T и τ приведены в таблице 1.

Таблица 1

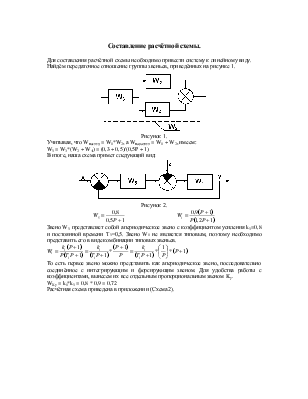
Составление принципиальной схемы.

Конечный выходной сигнал y получается на выходе первого звена. Входной сигнал первого звена получается путём суммирования выходных сигналов со второго и четвёртого звеньев с последующим вычитанием из них сигнала z. Таким образом, сигналы со второго и четвёртого звеньев подаются на сумматор с положительными знаками. С выхода сумматора сигнал идёт на вход другого сумматора, на другой вход которого с отрицательным знаком подаётся сигнал z. С выхода этого сумматора сигнал идёт на вход первого звена. Входные сигналы второго и четвёртого звеньев равны между собой и равны выходному значению третьего звена, следовательно, второе и четвёртое звено подключены параллельно. Входной сигнал третьего звена равен разности главного входного сигнала и главного выходного сигнала. Сигнал x поступает на сумматор с положительным знаком, а сигнал y - с отрицательным. Результат суммирования поступает в третье звено, с выхода которого сигнал подаётся на второе и четвёртое звено. Базовая схема приведена в приложении (Схема 1).

Расчёт передаточных функций.

Для первого элемента имеем:

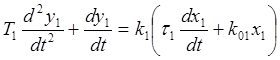
Подставим в это уравнение коэффициенты, равные нулю или единице. В результате получим:

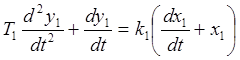
Произведём преобразование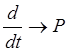

T₁P²y₁ + Py₁ = k₁(Px₁ + x₁)

Py₁(T₁P + 1) = k₁x₁(P + 1)

Выразим из этого уравнения y₁:

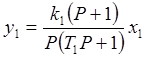
Передаточная функция первого звена равна

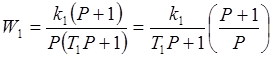
т.е. сложную передаточную функцию первого звена можно разложить на три простые передаточные функции типовых звеньев.

Для второго элемента:

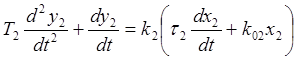
Подставим в это уравнение коэффициенты, равные нулю или единице. В результате получим:

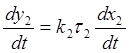
Произведём преобразование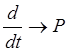

Py₂ = k₂τ₂Px₂, откуда y₂ = k₂τ₂x₂.

Второе звено является пропорциональным с коэффициентом усиления W₂ = k₂τ₂.

Для третьего элемента:

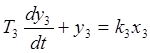
Подставим в это уравнение коэффициенты, равные нулю или единице и произведём преобразование 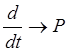. В результате получим:

Т₃Py₃ + y₃ = x₃, откуда y₃ = x₃/(T₃P+1)

Третье звено является апериодическим с передаточной функцией W₃ = 1/(T₃P+1)

Для четвёртого элемента:

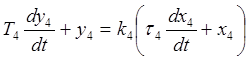
Подставим в это уравнение коэффициенты, равные нулю или единице. В результате получим:

y₄ = k₄x₄

Четвёртое звено является пропорциональным с коэффициентом усиления W₄ = k₄.

Итог:

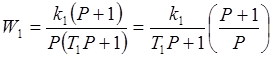
W₂ = k₂τ₂

W₃ = 1/(T₃P+1)

W₄ = k₄

Составление расчётной схемы.

Для составления расчётной схемы необходимо привести систему к линейному виду.

Найдём передаточное отношение группы звеньев, приведённых на рисунке 1.

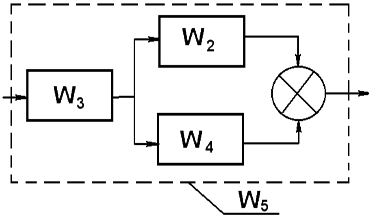
Рисунок 1.

Учитывая, что W_послед = W₁*W₂, а W_{параллел} = W₁ + W₂, имеем:

W₅ = W₃*(W₂ + W₄) = (0,3 + 0,5)/(0,5P + 1)

В итоге, наша схема примет следующий вид:

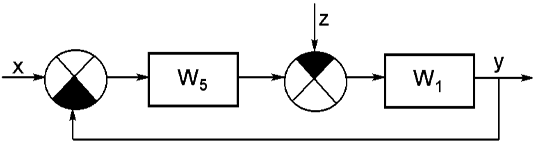
Рисунок 2.

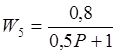
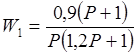
Звено W₅ представляет собой апериодическое звено с коэффициентом усиления k₅=0,8 и постоянной времени T₅=0,5. Звено W₁ не является типовым, поэтому необходимо представить его в виде комбинации типовых звеньев.

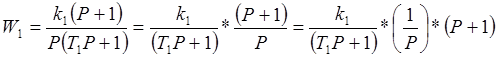
То есть первое звено можно представить как апериодическое звено, последовательно соединённое с интегрирующим и форсирующим звеном. Для удобства работы с коэффициентами, вынесем их все отдельным пропорциональным звеном K_у.

W_Kу = k₁*k₅ = 0,8 * 0,9 = 0,72

Расчётная схема приведена в приложении (Схема 2).

Построение компьютерной модели системы

По расчётной схеме 2 (см. Приложение) составляем компьютерную модель. Ступенчатый входной сигнал х создаётся звеном ступенчатого воздействия ВСТУП. Затем сигнал подаётся на положительный вход сумматора СУММ. С выхода сумматора сигнал идёт на усилительное звено ПРОПР с коэффициентом усиления К_у = 0,72. Затем идёт апериодическое звено АПЕРЗ с постоянной времени Т₅ = 0,5. Для организации внешнего воздействия z установим в систему звено ступенчатого воздействия ВСТУП.

Далее установим сумматор СУММ, на один вход которого с положительным знаком подаётся выходной сигнал с апериодического звена АПЕРЗ, а на другой - с отрицательным знаком сигнал z со звена ступенчатого воздействия ВСТУП. С выхода сумматора сигнал подаётся на другое апериодическое звено АПЕРЗ с постоянной времени Т₆ = 1,2. Далее сигнал идет на форсирующее звено ФОРСЗ и интегратор ИНТЕГ, на выходе которого получается выходной сигнал y, который подаётся на отрицательный вход первого сумматора.

В полученной системе задаём ступенчатый единичный входной сигнал х и запускаем постройку графиков x(t) и y(t) на одном рисунке.