Исследование системы автоматического управления на устойчивость, используя метод структурного моделирования

Новосибирский государственный технический университет

Кафедра электропривода и автоматизации промышленных установок

О Т Ч Ё Т

ПО ЛАБОРАТОРНОЙ РАБОТЕ

Дисциплина: «Теория автоматического управления»

Работа № 3

Наименование:    Исследование устойчивости линейных систем автоматического управления

Группа:                КП-21

Выполнил:           Пищинский К. В.

Работа защищена:__________________________________

Преподаватель:                     Нос О. В.                                   1

2005 г.

ЦЕЛЬ РАБОТЫ

Используя метод структурного моделирования, исследовать заданную систему автоматического управления на устойчивость. Установить влияние параметров системы на ее устойчивость и определить их граничные (критические) значения.

ИССЛЕДОВАИНЕ УСТОЙЧИВОСТИ ЛИНЕЙНОЙ СИСТЕМЫ

ПО КРИТЕРИЮ ГУРВИЦА

Определим устойчивость линейной системы, заданной на структурной схеме:

где k₁ = 8; k₂ = 5; k₃ = 3; T₁ = 3; T₂ = 5; T₃ = 0,1.

Найдем передаточную функцию систему:

;

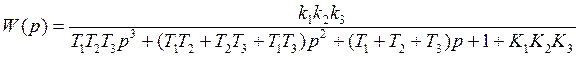Характеристическое уравнение будет           

Проверка по необходимому условию устойчивости:

1,5 > 0;

15,8 > 0;

8,1 > 0;

121 > 0;

все коэффициенты характеристического уравнения положительны – необходимое условие устойчивости выполняется.

Проверка по алгебраическому критерию устойчивости А. Гурвица:

–53,52 < 0;

2-й диагональный минор матрицы Гурвица отрицателен – условие не выполняется.

Линейная система не устойчива.

ИССЛЕДОВАНИЕ ВЛИЯНИЯ КОЭФФИЦИЕНТА ПЕРЕДАЧИ

НА УСТОЙЧИВОСТЬ СИСТЕМЫ

Исследуем данную линейную систему методом структурного моделирования по следующей схеме:

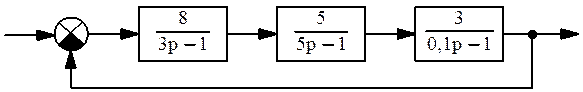
При заданных параметрах системы коэффициент передачи = 120.

Граничное значение коэффициента передачи определим из условия:

;

 k_ГР = 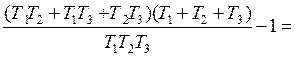84,32

Графики переходной функции при разных значениях коэффициента передачи:

Исходная переходная характеристика САУ k = 120
k = 200 > kГР
k = 84,32 = kГР
k = 40 < kГР

Вывод: при k < k_ГР линейная система устойчива; k = k_ГР при система находится на границе устойчивости; при k > k_ГР, линейная система неустойчива.

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ПОСТОЯННОЙ ВРЕМЕНИ T₃

НА УСТОЙЧИВОСТЬ СИСТЕМЫ

Граничные значение постоянной времени T₃ определим из условия:

;

Решим для этого квадратное уравнение:      

 = 0,069;     = 216,93.

Графики переходной функции при разных значениях постоянной времени T₃:

T3 = 0,02 <
T3 = 0,069 =
T3 = 111  < T3  <
T3 = 216,93 =
T3 = 666 >

Вывод: при T₃ <  и при T₃ >  линейная система устойчива;

при T₃ =  и T₃ =   система находится на границе устойчивости;

при  < T₃  <  линейная система неустойчива.

ИССЛЕДОВАИНЕ УСТОЙЧИВОСТИ ЛИНЕЙНОЙ СИСТЕМЫ

ПО КРИТЕРИЮ НАЙКВИСТА

Разомкнем линейную систему и исследуем методом структурного моделирования по схеме:

Найдем частоты сопряжения звеньев, входящих в разомкнутую систему:

0,333;       0,25;     10.

Частотные характеристики линейной разомкнутой системы:

ω	0	0,125	= 0,25	= 0,333	5	= 10
A(ω)	120	97,4	62,3	41,9	0,277	0,056
φ(ω)	0	–52,7	–89,7	–106,3	–199,8	–220,1

Также их можно получить аналитически по формулам:

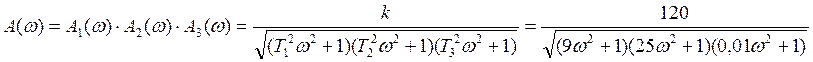
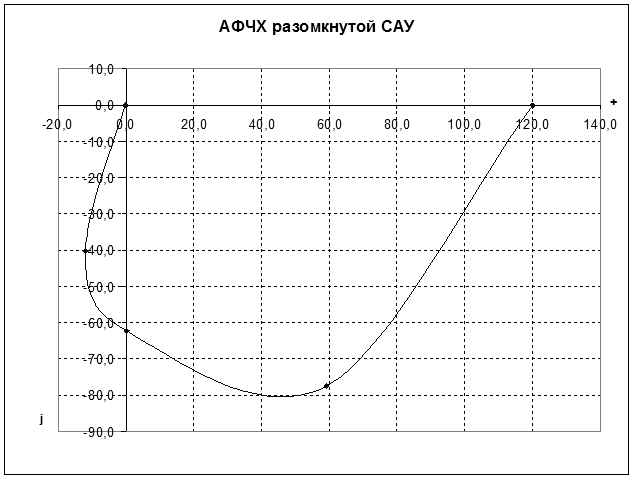
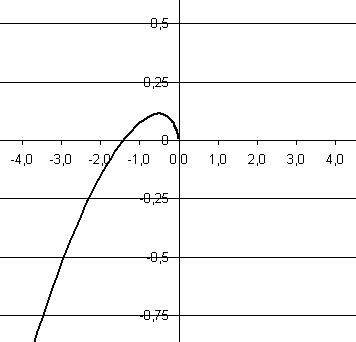
Вывод:

АФЧХ рассматриваемой линейной системы охватывает точку [–1+j·0] на вещественной оси, то есть при φ(ω) = –180° АФЧХ проходит слева от этой точки. Необходимое условие по критерию устойчивости Найквиста не выполняется, следовательно, исследуемая замкнутая линейная система не устойчива.

ВЫВОДЫ

Исследование устойчивости линейной системы методом структурного моделирования позволяет сопоставить разные критерии устойчивости, а так же изучить влияние параметров линейной системы на ее устойчивость.