Необходимое условие устойчивости линейных непрерывных систем. Критерий устойчивости Рауса. Критерий устойчивости Гурвица. Критерий устойчивости Льенара – Шипаро

24. Необходимое условие устойчивости линейных непрерывных систем. Критерии устойчивости линейных непрерывных САР. Критерий устойчивости Рауса. Критерий устойчивости Гурвица. Критерий устойчивости Льенара – Шипаро.

Необходимое условие устойчивости линейных непрерывных систем

Характеристическое уравнение в общем виде

можно разложить на произведение множителей первого порядка:

 

Если все корни являются отрицательными и вещественными               , то тогда

Все коэффициенты D(р) будут положительными, в противном случае, если есть один или несколько положительных корней                                                         , тогда                                                           , то имеет место хотя бы один отрицательный коэффициент D(р).

При комплексно-сопряженных корнях с отрицательной вещественной частью                            :

                                                                                                                                     ,

что опять приводит к положительности всех коэффициентов D(р).

Таким образом, необходимым условием(условие А. Стодолы) устойчивости линейных непрерывных систем является положительность всех коэффициентов характеристического уравнения           , причем, все вещественные корни, если они есть, будут отрицательны.

В противном случае, необходимо применять дополнительные процедуры для нахождения знака вещественной части корней, чтобы сделать вывод об устойчивости, т.к. для случая чисто мнимых корней                                          , также имеет место           .

Определение. Критериями устойчивости называются правила, позволяющие исследовать устойчивость без непосредственного нахождения корней характеристического уравнения, подразделяющиеся на алгебраические и частотные.

Алгебраические критерии устойчивости оперируют с коэффициентами характеристического уравнения, на основании которых делается вывод о знаке вещественных частей корней D(p).

Частотные критерии позволяют судить об устойчивости по виду частотных характеристик в различных масштабах и имеют простую геометрическую интерпретацию и наглядность.   

Алгебраические критерии устойчивости

Критерий устойчивости Рауса.  Для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т.е. при a₀ > 0 были положительными числа:

 

Критерий, который предложил Раус, наиболее просто поясняется таблицей Рауса, где

                                                          характеристический полином.

                    Таблица Рауса

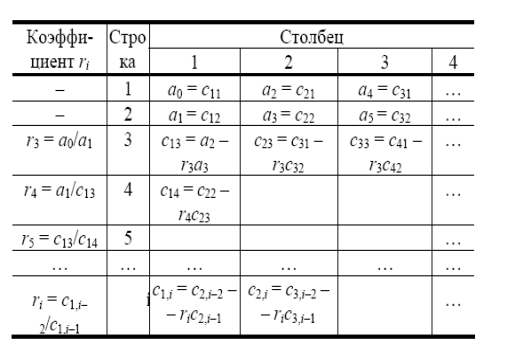В первой строке записываются в порядке

 возрастания индексов коэффициенты

характеристического уравнения,

имеющие четный индекс,

во второй − нечетный индекс.

Любой другой коэффициент таблицы

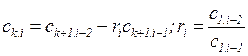определяется как

                                                             ,

где k - номер столбца; i - номер строки.

Число строк таблицы Рауса равно

степени характеристического полинома

плюс единица – (n + 1).

Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней равно числу перемен знака в первом столбце таблицы Рауса.

Этот критерий очень удобен, когда заданы численные значения коэффициентов характеристического уравнения, очень легок для программирования на ЭВМ и нашел широкое применение при исследовании влияния на устойчивость коэффициентов уравнения либо отдельных параметров системы.

Критерий устойчивости Гурвица. Для того чтобы линейная непрерывная система была устойчива, необходимо и достаточно, чтобы главный определитель матрицы Гурвица и все его  диагональные миноры были положительными:

                                              Δ₁ > 0, Δ₂ > 0, …………, Δ_n > 0.

Определение. Матрица Гурвица – это матрица размерности         , элементами которой являются коэффициенты характеристического уравнения D(p) и нули.

Порядок заполнения матрицы Гурвица

1. По главной диагонали выписываются коэффициенты характеристического уравнения, начиная с a₁ по a_n в возрастающем порядке.

2. Вверх от главной диагонали записываются коэффициенты D(p) с возрастающими индексами, а вниз с убывающими.

3. Свободные места в матрице Гурвица заполняются нулями.

                 

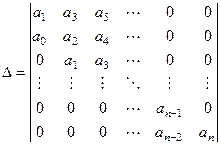
                       Матрица Гурвица

Из структуры матрицы Гурвица (определителя Гурвица), в последнем столбце только один коэффициент отличен от нуля, в результате чего n- ый диагональный минор (определитель матрицы Гурвица) находится как

откуда при a_n > 0 (необходимое условие устойчивости) и Δ_n-1 > 0 он автоматически становится положительным. По этой причине на практике вычисляют только n - 1 диагональный минор.

Применение алгебраического критерия Гурвица для линейных систем до 5–ого порядка включительно.

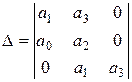1. n = 3.

Тогда

Следовательно должно соблюдаться             ,                                  или                    .

2. n = 4.

 

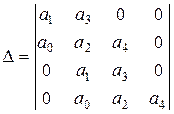Матрица (определитель) Гурвица:

Откуда:

 

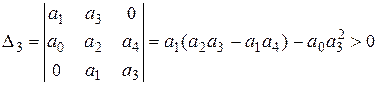
                                                                                                    или

Учитывая, что диагональный минор третьего порядка будет положительным только при Δ₂ > 0, то общее условие устойчивости для САР с n = 4 будет иметь место только при проверке лишь одного последнего неравенства, а именно

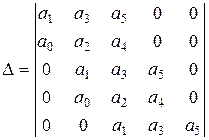3. n = 5.

Матрица (определитель) Гурвица:

Система будет устойчива, если :           

 

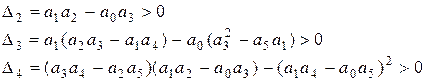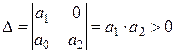Из критерия Гурвица видно, что для линейных систем не выше второго порядка необходимое условие устойчивости является также и достаточным, т.е.

На основании алгебраического критерия Гурвица можно выделить области устойчивого и неустойчивого состояний линейной непрерывной системы.