Необходимое условие устойчивости линейных непрерывных систем. Критерий устойчивости Рауса. Критерий устойчивости Гурвица. Критерий устойчивости Льенара – Шипаро, страница 3

В соответствии с теоремой Безу характеристический полином произвольного порядка можно разложить на произведение элементарных скобок:

Величина                 геометрически представляет собой вектор, проведенный из      к произвольной точке р.

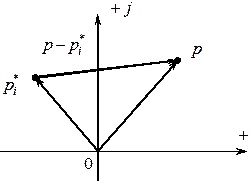
          Пространственное расположение вектора               на комплексной плоскости

Принцип аргумента. Для упрощения анализа произвольную точку принимают на мнимой положительной полуоси             :

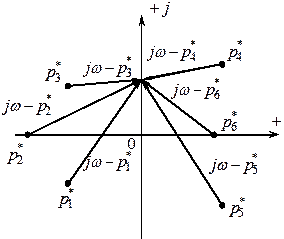В этом случае концы всех элементарных векторов будут находиться на мнимой оси.

         Пространственное положение

         элементарных векторов при

         выборе точки  на мнимой

         положительной полуоси

Величина D(jw) представляет собой вектор параметры которого определяются как:

•  модуль                                                                                                         ;

 

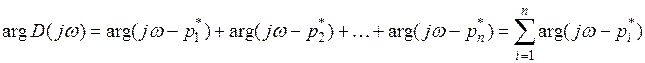
•  фаза                                                                                                                    .

Рассмотрим, на какой угол поворачивается элементарный вектор

при изменении частоты от 0 до     .

Пусть корень является вещественным, как положительным, так и отрицательным            

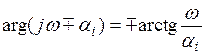
Тогда для каждой скобки в выражении для фазы D(jw) становится справедливым                ,

откуда

 

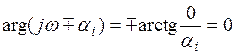При нулевой частоте ω = 0 фазовый сдвиг равен:

 

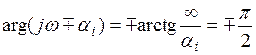При           фазовый сдвиг равен:

В итоге, при изменении частоты ω от 0 до       элементарный вектор повернется при

отрицательном вещественном корне                 на угол         , а при положительном корне      

на угол            .

Пусть в характеристическом уравнении присутствует пара комплексно-сопряженных корней с отрицательной вещественной частью                          , откуда в D(jw) входят следующие скобки:

Рассмотрим, какой суммарный фазовый сдвиг дает произведение двух последних преобразованных скобок при изменении частоты от 0 до      .   

При ω  = 0

где γ  – некоторый начальный угол, зависящий от соотношения мнимой и вещественной

частей         .

При ω =                                                        , откуда суммарный угол поворота от действия двух

комплексно-сопряженных корней с отрицательной вещественной частью:

По аналогии, для пары комплексно-сопряженных корней с положительной вещественной частью суммарный поворот элементарных векторов                   и                    при изменении частоты от 0 до         

      составляет - π .

Суммарный аргумент вектора D(jw) при изменении частоты от 0 до     определяется как сумма углов поворота векторов                  и при n корнях с отрицательной вещественной частью

 

а при наличии k «правых» корней находится как

26. Частотные критерии устойчивости. Критерий устойчивости Михайлова.

Частотный критерий А.В. Михайлова. Для устойчивости линейной непрерывной системы необходимо и достаточно, чтобы при изменении частоты от 0 до    годограф Михайлова, начинаясь с положительной вещественной полуоси, последовательно обходил против часовой стрелки n квадрантов комплексной плоскости, где n – порядок характеристического уравнения, и при этом нигде не обращался в ноль.

Годограф Михайлова получается путем замены в характеристическом уравнении D(p) оператора дифференцирования р на оператор jw(р ↔ jw):

Последнее выражение можно также представить в виде

                                                                                                                    ,

где       – корень характеристического уравнения.

Рассмотрим, как влияют различные корни на вид годографа Михайлова.

Если все корни содержат в себе отрицательную вещественную часть, то годограф Михайлова при ω  = 0  начинается на положительной вещественной оси в точке a_n.