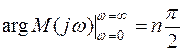 При изменении частоты ω от 0 до ∞
годограф Михайлова делает суммарный поворот:
При изменении частоты ω от 0 до ∞
годограф Михайлова делает суммарный поворот:
![]()
![]() Действительно, если все корни
отрицательные и вещественные, причем выполняется необходимое условие
устойчивости , то .
Действительно, если все корни
отрицательные и вещественные, причем выполняется необходимое условие
устойчивости , то .
![]()
![]() Если корни
комплексно-сопряженные или чисто мнимые, то
Если корни
комплексно-сопряженные или чисто мнимые, то
и ,
т.е. при нулевой частоте М(0) будет также положительным.
Для определения числа «правых» корней по виду годографа Михайлова с остальными «левыми» необходимо воспользоваться принципом аргумента, на основании которого при k корнях D(p) с положительной вещественной частью справедливо равенство:
Из данного выражения можно определить количество квадрантов, которые последовательно обошел годограф А.В. Михайлова нигде не обращаясь в начало координат при изменении частоты
![]() .
.
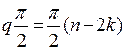
![]() Количество
квадрантов
q, которые
последовательно обошел годограф А.В. Михайлова нигде не обращаясь в начало
координат при изменении частоты :
Количество
квадрантов
q, которые
последовательно обошел годограф А.В. Михайлова нигде не обращаясь в начало
координат при изменении частоты :
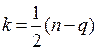
Отсюда количество «правых» корней характеристического уравнения равно: .
![]() При наличии одного или несколько
нулевых корней становится справедливым следующее выражение для годографа
Михайлова: ,
При наличии одного или несколько
нулевых корней становится справедливым следующее выражение для годографа
Михайлова: ,
где r - количество нулевых корней.
![]() В результате чего при последнее равенство
обращается в 0, т.е и годограф Михайлова выходит из
начала координат.
В результате чего при последнее равенство
обращается в 0, т.е и годограф Михайлова выходит из
начала координат.
![]() Если САР находится на границе устойчивости,
которой соответствует произведение
Если САР находится на границе устойчивости,
которой соответствует произведение
![]() ,
,
то на частоте равной величине β годограф Михайлова обратиться в 0, т.е. пройдет через начало координат.
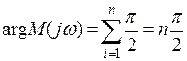 В итоге, при наличии во всех корнях
отрицательных вещественных частей годограф Михайлова при изменении частоты
входного гармонического сигнала от 0 до ∞ последовательно против часовой
стрелки обойдет п квадрантов:
В итоге, при наличии во всех корнях
отрицательных вещественных частей годограф Михайлова при изменении частоты
входного гармонического сигнала от 0 до ∞ последовательно против часовой
стрелки обойдет п квадрантов:
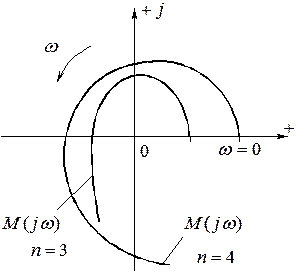
Годографы Михайлова для устойчивой линейной системы с различными порядками D(p).
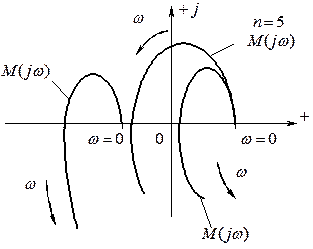
Годографы Михайлова неустойчивых САР
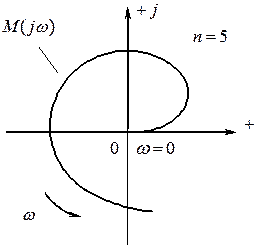
Годограф Михайлова нейтрально устойчивой САР при r = 1
и n = 5.
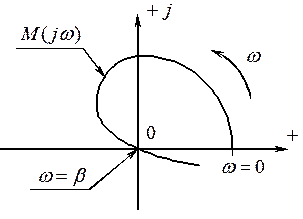
Годограф Михайлова в случае пары чисто мнимых корней.
В практических приложениях нет необходимости строить полную кривую Михайлова, а достаточно ограничиться лишь нахождением ее точек пересечения с координатными осями комплексной плоскости и определением соответствующих частот, для чего предварительно необходимо представить годограф в алгебраической форме функции комплексного переменного как
Если в результате расчетов численные значения частот получаются мнимыми, то это соответствует случаю, когда кривая не пересекает данную ось.
![]() Пример. Определить
устойчивость линейной непрерывной САР третьего порядка на основании частотного
критерия А.В. Михайлова, характеристическое уравнение которой задано в
следующем виде:
Пример. Определить
устойчивость линейной непрерывной САР третьего порядка на основании частотного
критерия А.В. Михайлова, характеристическое уравнение которой задано в
следующем виде:
![]() Годограф Михайлова описывается зависимостью:
Годограф Михайлова описывается зависимостью:
![]() Для определения частот, в которых происходит
пересечение кривой Михайлова с вещественной осью, приравняем мнимую часть М(jw) к нулю:
Для определения частот, в которых происходит
пересечение кривой Михайлова с вещественной осью, приравняем мнимую часть М(jw) к нулю:
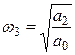
![]()
![]() Отбрасывая
отрицательное значение, которое не входит в диапазон изменения
частот ,
Отбрасывая
отрицательное значение, которое не входит в диапазон изменения
частот ,
окончательно получаем: , .
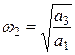 По аналогии, в точке пересечения годографа с мнимой
осью, соответствующая частота находится как
По аналогии, в точке пересечения годографа с мнимой
осью, соответствующая частота находится как
![]() , откуда
.
, откуда
.
![]() Подставляя найденные величины w1 и w3 в PM (w) , а ω2 в QM (w) , строится
годограф Михайлова, причем если выполняется неравенство вида
, то исследуемая линейная САР будет устойчивой.
Подставляя найденные величины w1 и w3 в PM (w) , а ω2 в QM (w) , строится
годограф Михайлова, причем если выполняется неравенство вида
, то исследуемая линейная САР будет устойчивой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.