Необходимое условие устойчивости линейных непрерывных систем. Критерий устойчивости Рауса. Критерий устойчивости Гурвица. Критерий устойчивости Льенара – Шипаро, страница 2

Границе устойчивости (пара чисто мнимых корней или нулевой корень) будет соответствовать равенство:                        или

Это соответствует незатухающим гармоническим автоколебаниям на выходе при положительности всех до n = 2 диагональных миноров включительно, либо при нейтральной устойчивости (           ) в случае a_n = 0.

В свою очередь число «правых» корней равно количеству перемен знака в приведенной ниже последовательности:    a₀, Δ₁, Δ₂ , …………, Δ_n-1 , a_n,

причем при этом должно соблюдаться неравенство:

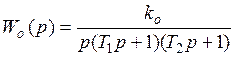Пример. Рассмотрим области устойчивого состояния замкнутой САР линейным объектом третьего порядка, имеющей следующую передаточную функцию:

где k_o  – коэффициент передачи объекта управления.

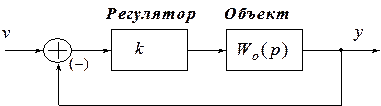
Характеристическое уравнение замкнутой САУ с пропорциональным регулятором k в данном случае будет находиться как

                – коэффициент САУ в разомкнутом состоянии.

Характеристическое уравнение данной системы в общем виде: 

На основании алгебраического критерия устойчивости А. Гурвица в D(p) будут присутствовать корни с отрицательной вещественной частью при выполнении следующего неравенства:

                                       ,                              или

Граница нейтральной устойчивости будет иметь место в случае                  , а паре чисто мнимых корней соответствует:                                       ,                     ,                      ,

где k_гр  – граничное значение коэффициента передачи системы в разомкнутом состоянии.

Можно графически изобразить область устойчивости в одномерном пространстве коэффициента k_p.

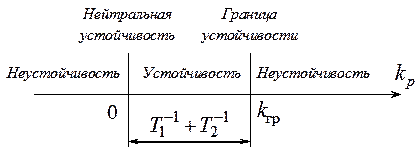
Области устойчивости и неустойчивости исходной замкнутой САP в функции коэффициента k_p.

Критерий устойчивости Льенара – Шипаро.  Для того, чтобы система автоматического управления была устойчивой, необходимо и достаточно, чтобы выполнялось необходимое условие устойчивости и чтобы определители Гурвица с четными индексами (или с нечетными индексами) были положительны, т.е.   a₀ > 0, a₁ > 0, …., a_n > 0, Δ₂ > 0, Δ₄ > 0, Δ₆ > 0 …      или

a₀ > 0, a₁ > 0, …., a_n > 0, Δ₁ > 0, Δ₃ > 0, Δ₅ > 0, …

В такой формулировке критерия устойчивости требуется раскрытие меньшего числа определителей, чем по критерию Гурвица.

Область устойчивости системы

Определение. Геометрический образ зависимости устойчивости от параметров системы называется областью устойчивости.

Область устойчивости строится в пространстве параметров, под которым понимается пространство, координатами которого являются параметры системы.

Количество параметров может быть любым, но для графического изображения наиболее распространенными являются два.

Пусть характеристическое уравнение системы имеет вид:

где А и В – параметры системы.

Для устойчивости системы, исходя из критерия Гурвица, необходимо и достаточно, чтобы

А В > 1, откуда граница области устойчивости будет А В = 1.

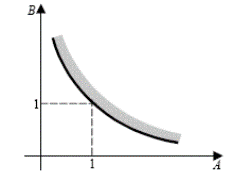В плоскости параметров A и В граница области устойчивости представляет собой гиперболу, называемую гиперболой Вышнеградского.

                       Область устойчивой работы

                         отмечена штриховкой

Границы области устойчивости могут быть найдены, если приравнять нулю коэффициенты а₀, а_n характеристического уравнения и предпоследний определитель Гурвица:

a₀ = 0,  a_n = 0, Δ_n-1 = 0.

Вторая из этих границ соответствует наличию нулевого корня характеристического уравнения, а третья − наличию чисто мнимых корней.

Последние уравнения разбивают пространство параметров на ряд областей, из которых устойчивой будет та область, где определители Гурвица Δ₁, ..., Δ_n–2 положительны.

25. Частотные критерии устойчивости. Принцип аргумента.

Частотные критерии устойчивости

Принцип аргумента. Каждый корень характеристического уравнения     можно изобразить на комплексной плоскости в виде вектора, проведенного из начала координат, амплитуда которого равна модулю комплексного числа, а фаза, отсчитываемая от положительной вещественной оси, равна аргументу.