Для анализа реакции системы на возмущающее воздействие z установим единичный ступенчатый входной сигнал z и запустим постройку графиков x(t), z(t) и y(t) на одном рисунке.
Для определения статической ошибки подадим на вход системы линейно возрастающий сигнал. Для этого сразу после первого генератора ступенчатого воздействия ВСТУП поставим интегрирующее звено ИНТЕГ. В полученной системе задаём ступенчатый единичный входной сигнал х и запускаем постройку графиков x(t) и y(t) на одном рисунке. Сигнал z при этом следует отключить. Статическая ошибка будет равна разнице ординат входного сигнала х и выходного у. Для анализа зависимости статической ошибки от возмущающего воздействия z установим единичный ступенчатый входной сигнал z и запустим постройку графиков x(t), z(t) и y(t) на одном рисунке.
Построение ЛАЧХ системы
Преимущество логарифмической амплитудно-частотной характеристики заключается в том, что на небольшом участке можно разместить большой диапазон частот. Строить ЛАХ системы проще по частям, сначала построив ЛАХ типовых звеньев, входящих в неё. Затем, просуммировав графики, мы получим ЛАХ исходной системы.
ЛАХи типовых звеньев, входящих в состав системы, будут следующими:
Пропорциональное звено - прямая, параллельная оси абсцисс, отстоящая от неё на величину Lпр = 20lgKy = -2,85 дБ
Апериодическое звено - ломаная линия, на участке от нуля до ω=1/Т прямая, параллельная оси абсцисс, отстоящая от неё на величину L0ап = 20lgk, а при ω>1/Т - прямая, убывающая со скоростью 20 дБ/дек. В нашем случае для обоих апериодических звеньев k = 1, следовательно, на участке от нуля до ω=1/Т график ЛАХ совпадает с осью абсцисс. Частоты изгиба для пятого и шестого (по обозначению в схеме 2) соответственно ω5И = 1/Т5 = 2 Гц, ω6И = 1/Т6 = 2 Гц.
Форсирующее звено - ломаная линия, на участке от нуля до ω=1/τ прямая, параллельная оси абсцисс, отстоящая от неё на величину L0фор = 20lgk, а при ω>1/τ - прямая, возрастающая со скоростью 20 дБ/дек. В нашем случае k = 1, следовательно, на участке от нуля до ω=1/τ график ЛАХ совпадает с осью абсцисс. Частота изгиба графика ωИ = 1.
Интегрирующее звено представляет собой прямую, пересекающую ось абсцисс в точке ω=1 и убывающую со скоростью 20 дБ/дек.
По этим данным строим ЛАХ типовых звеньев (обозначены чёрным цветом). После построения ЛАХ типовых звеньев производим их суммирование. В результате получаем ЛАХ системы (обозначена красным цветом и имеет соответствующую подпись). График ЛАЧХ находится в приложении.
Анализ системы
1. Определение быстродействия системы.
Для определения быстродействия системы по ЛАЧХ нам необходимо знать частоту среза. ωср ≈ 0,72 Гц. Тогда время переходного процесса определится по формуле:
tпп = π/ωср = 4,4 с.
2. Нахождение передаточной функции разомкнутой системы.
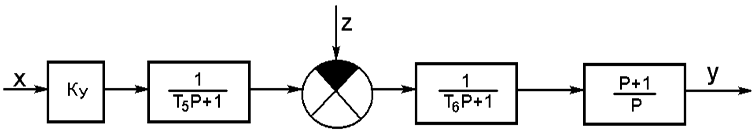
Рисунок 3
Передаточная функция разомкнутой системы будет равна произведению передаточных функций, лежащих между входом в систему и местом размыкания. Разомкнём систему на линии обратной связи. В результате получим разомкнутую схему (рисунок 3), передаточная функция которой будет равна:
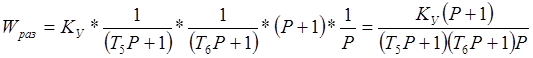
3. Передаточные функции замкнутой системы.
Передаточная функция от одной точки замкнутой цепи элементов до другой равна передаточной функции элементов, лежащих между этими точками при движении по ходу сигнала, делённой на передаточную функцию разомкнутой системы, увеличенной на единицу.
Таким образом, передаточные функции замкнутой системы определятся следующим образом:
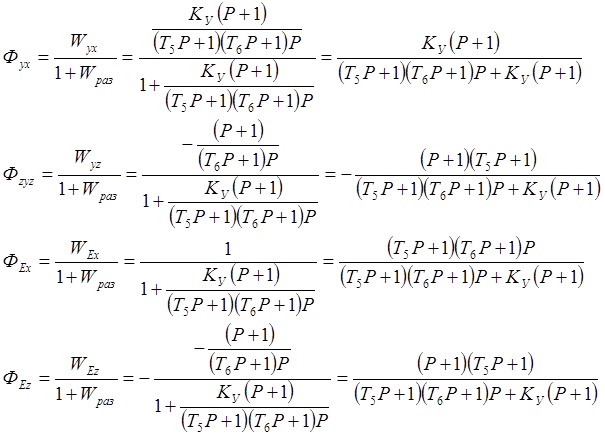
4. Определение статической ошибки.
Статическая ошибка системы по задающему воздействию определяется по формуле:
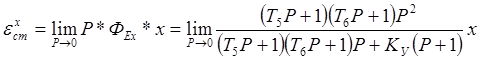
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.