Анализ системы, определение динамических и статических показателей качества системы, страница 3

Для единичного ступенчатого воздействия х = 1/Р имеем:

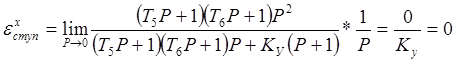
Для линейно возрастающей функции х = 1/Р² имеем:

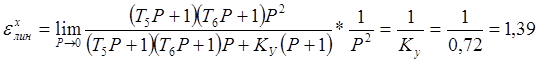
Статическая ошибка системы по возмущающему воздействию определяется по формуле:

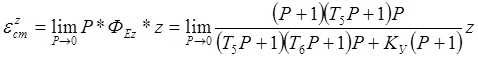
Для единичного ступенчатого воздействия z = 1/Р имеем:

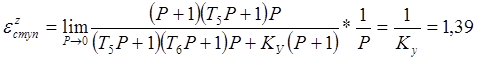
Для линейно возрастающей функции z = 1/Р² имеем:

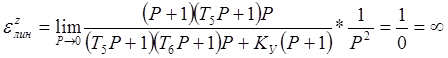
Суммарная статическая ошибка при ступенчатом задающем и возмущающем воздействии ε_ст = ε^x_ступ +ε^z_ступ = 0 + 1,9 = 1,9

Суммарная статическая ошибка при линейном задающем и ступенчатом возмущающем воздействии ε_ст = ε^x_лин +ε^z_ступ = 1,9 + 1,9 = 3,8

5. Определение устойчивости системы.

Запишем уравнение функции y = f(x):

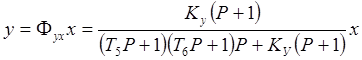
Преобразуем систему:

Оператроный полином при выходной координате имеет вид:

Откуда по критерию Гурвица и Рауса получаем

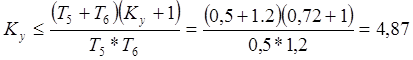
Синтез корректирующего звена

1. Требования к системе.

По заданию нам нужно увеличить быстродействие системы в 10 раз. Частоту среза исходной системы ω_ср ≈ 0,72 Гц. Зададимся частотой среза желаемой системы:

ω_ср^жел = 8 Гц.

Тогда t_пп^жел = π/ω_ср^жел = 0,4 с.

Статическая ошибка желаемой системы не должна превышать 0,05.

Тогда К_у^жел = 1/0,05 = 20. Такое значение коэффициента без введения корректирующего звена приведёт к потери устойчивости.

2. Определение ЛАЧХ желаемой системы.

На графике, где изображена ЛАХ исходной системы, строим ЛАХ желаемой системы. Для этого через точку ω_ср^жел = 8 Гц проводим прямую, убывающую со скоростью 20дБ/дек. Эта прямая пересечёт ось ординат в точке L = 38,5 дБ.

Проведём прямую, параллельную оси абсцисс и лежащую на 15 дБ ниже её. Обозначим точку пересечения этой прямой с прямой, пересекающей ось абсцисс в точке ω_ср = 8 Гц. В результате ЛАХ желаемой системы будет выглядеть следующим образом: при ω < 8 Гц - прямая убывающая со скоростью 20дБ/дек, а при ω > 8 Гц - прямая, убывающая со скоростью 40дБ/дек. ЛАЧХ желаемой системы обозначена на графике красным цветом и имеет соответствующую подпись.

3. Определение ЛАЧХ корректирующего звена.

Возможны 2 варианта ЛАХ корректирующего звена.

Для получения первого варианта ЛАХ корректирующего звена достаточно вычесть из графика желаемой функции график исходной системы. Первый вариант ЛАЧХ корректирующего звена обозначена на графике зелёным цветом и римской цифрой I.

Для получения второго варианта просто упростим первый, сделав участок от ω = 0,1 до ω = 2 горизонтальным, без ступеньки на участке (5/6…1). Второй вариант ЛАЧХ корректирующего звена обозначена на графике зелёным цветом и римской цифрой II.

4. Определение передаточной функции корректирующего звена.

Вариант I

Коэффициент усиления корректирующего звена будет равен К_кор = 10^21,35/20 = 11,68.

В точке ω = 5/6 Гц установим форсирующее звено. τ = 1,2. W = (1,2Р+1)

В точке ω = 1 Гц установим апериодическое звено. Т = 1. W = (1/(Р+1))

В точке ω = 2 Гц установим форсирующее звено. τ = 0,5 W = (0,5Р+1)

В точке ω = 14 Гц установим апериодическое звено. Т = 0,07. W = (1/(0,07Р+1))

В результате передаточная функция корректирующего звена будет иметь вид:

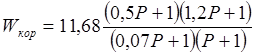
Вариант II.

Коэффициент усиления корректирующего звена примем К_кор = 12

В точке ω = 2 Гц установим форсирующее звено. τ = 0,5 W = (0,5Р+1)

В точке ω = 14 Гц установим апериодическое звено. Т = 0,07. W = (1/(0,07Р+1))

В результате передаточная функция корректирующего звена будет иметь вид:

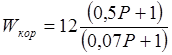
Моделирование скорректированной системы на компьютере

К имеющейся у нас модели исходной системы сразу после первого сумматора, перед первым (по счёту) апериодическим звеном устанавливаем корректирующее звено. Корректирующее звено является сложным, но его можно разложить на несколько типовых. Эта процедура уже была описана выше.