Моделирование первого варианта.
В результате введения первого варианта корректирующего звена у нас заметно уменьшился переходной процесс, однако система стала колебательной. По заданию такой вариант недопустим.
Моделирование второго варианта.
В результате введения второго варианта корректирующего звена у нас при отработке ступенчатого на порядок уменьшился переходной процесс, система не стала колебательной, перерегулирование не превышает 5%. При отработке линейно возрастающего сигнала статическая ошибка тоже заметно уменьшилась. Графики, полученные при установке второго варианта корректирующего звена, приведены далее.
Анализ скорректированной системы
1. Определение быстродействия системы.
Для определения быстродействия системы по ЛАЧХ нам необходимо знать частоту среза. ωср = 8 Гц. Тогда время переходного процесса определится по формуле:
tпп = π/ωср = 0,4 с.
2. Нахождение передаточной функции разомкнутой системы.
Передаточная функция разомкнутой системы будет равна произведению передаточных функций, лежащих между входом в систему и местом размыкания.
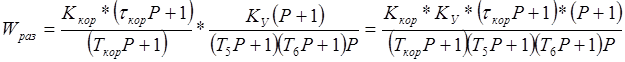
Подставив числовые значения коэффициентов и сократив дробь, получим:
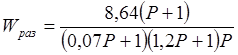
3. Передаточные функции замкнутой системы.
Передаточная функция от одной точки замкнутой цепи элементов до другой равна передаточной функции элементов, лежащих между этими точками при движении по ходу сигнала, делённой на передаточную функцию разомкнутой системы, увеличенной на единицу.
Таким образом, передаточные функции замкнутой системы определятся следующим образом:
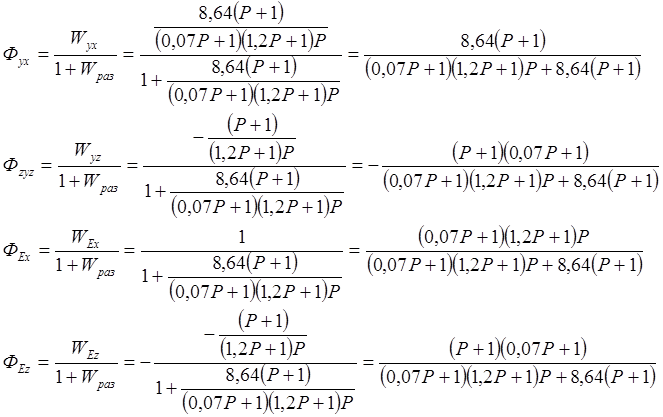
4. Определение статической ошибки.
Статическая ошибка системы по задающему воздействию определяется по формуле:
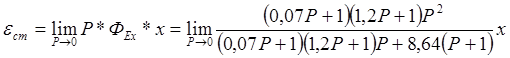
Для единичного ступенчатого воздействия х = 1/Р имеем:
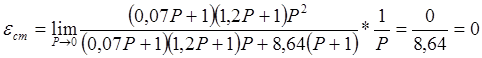
Для линейно возрастающей функции х = 1/Р2 имеем:
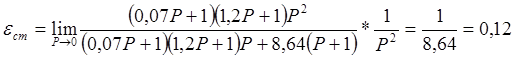
Статическая ошибка системы по возмущающему воздействию определяется по формуле:
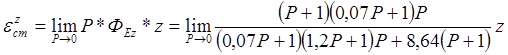
Для единичного ступенчатого воздействия z = 1/Р имеем:
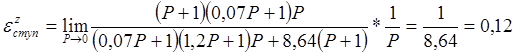
Для линейно возрастающей функции z = 1/Р2 имеем:
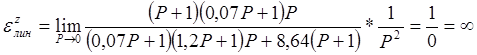
Суммарная статическая ошибка при ступенчатом задающем и возмущающем воздействии εст = εxступ +εzступ = 0 + 0,12 = 0,12
Суммарная статическая ошибка при линейном задающем и ступенчатом возмущающем воздействии εст = εxлин +εzступ = 0,12 + 0,12 = 0,24
5. Определение устойчивости системы.
Запишем уравнение функции y = f(x):
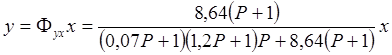
Преобразуем систему:
![]()
Оператроный полином при выходной координате имеет вид:
![]()
Откуда по критерию Гурвица и Рауса получаем
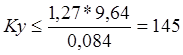
Вывод
В результате проделанной работы было подобрано простое, но очень эффективное корректирующее звено. Время переходного процесса уменьшилось на порядок, статическая ошибка тоже. Также заметно снизилось влияние внешнего возмущающего воздействия. В процессе работы было обнаружено, что попытка максимально сгладить ЛАХЧ системы привела к возникновению колебательных процессов в системе. Упрощение корректирующего звена наоборот привело к улучшению характеристик системы.
Список литературы
1. Теория автоматического управления: Учебник для вузов по специальностям "Технология машиностроения" и "Металлорежущие станки и инструменты" Под ред. Ю.М. Соломенцева - М.: Машиностроение, 1992.
2. Основы автоматического регулирования и управления. Под ред. В.М. Понномарёва и А.П. Литвинова - М.: Высшая школа, 1974.
3. Основы автоматики: рабочая программа и методические указания к выполнению расчётно-графических и курсовых работ. В.И. Сивачек, В.И. Каплин, Я.Н. Троицкий - Новосибирский государственный технический университет, 1997.
4. В.В. Панкратов: Программа структурного моделирования динамических систем "КОМПАС" - Новосибирский государственный технический университет, 1994.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.