Анализ и синтез механизма зубострогального станка для нарезания конических колес, страница 5

Рассматриваем движение точки D. Эта точка совершает вращательное движение, участвует в поступательном движении вдоль звена 3 и движется поступательно относительно звена 5. Поэтому векторное уравнение будет выглядеть так: . - скорость вращательного движения относительно звена 3 направляется перпендикулярно CD, модуль определяется по формуле: ,  направляем параллельно CD,  - параллельно линии ED. Данное уравнение также решаем графически. Именно с плана скоростей берем неизвестные величины скоростей, умножая их на масштабный коэффициент, величина которого .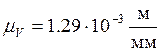

            После того, как построен план скоростей, можем определить угловые и линейные скорости.

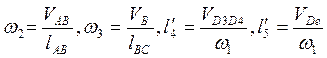                                                                            (2.27)

            Тогда: ;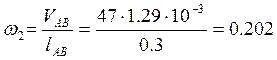

; .

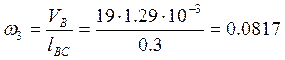
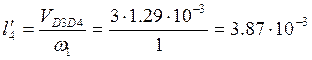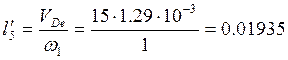            Определяем ускорения графически.

Как и для скоростей, для ускорений в произвольном месте чертежа выбираем полюс плана ускорений . Необходимо также ввести масштабный коэффициент .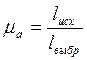

            Рассматриваем движение точки A. Для точки A есть одна составляющая ускорения – нормальная, параллельная AO. Модуль вектора определяется так: . При построении этого вектора выбираем произвольный отрезок , соответствующий рассматриваемому вектору, и рассчитываем масштабный коэффициент ускорений.

            Точка B.

Векторное уравнение ускорений точки B имеет вид: , где  - ускорение относительно точки A (нормальная составляющая параллельна AB, а касательная – перпендикулярна AB), а  - ускорение относительно точки C. Модули ускорений определяются так:  (аналогично и для ускорения ). Неизвестные определяем из графического решения векторного уравнения.

 

Точка D.

Данная точка участвует в нескольких движениях сразу. Будем обозначать:

- вращательное движение, - поступательное движение вместе с кулисой,

 - поступательное движение относительно звена 5. Тогда векторное уравнение ускорений будет иметь вид: , где  - ускорение Кориолиса.

Модули ускорений определяем так:  (здесь используем величину , полученную ранее из решения ).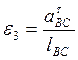

Далее графически определяем угловые и линейные ускорения.

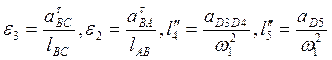                                                                           (2.28)

2.3.3. Результат

            В результате решения графическим и аналитическим методами получим таблицу 2.3 для аналогов скоростей и таблицу 2.4 для аналогов ускорений для двух расчетных углов. Как видно из таблиц, приведенных ниже, результаты расчета разными методами различаются незначительно.

Таблица 2.3.                                                                          Аналоги скоростей

Величина				, м	, м
Графически	0.202	0.0817	0.0817		0.01935
Аналитически	-0.208	0.079	0.079		-0.017
Отклонение,	2.88	3.41	3.41	1.12	11.7
Графически	0.2193	0.043	0.043
Аналитически	0.216	0.046	0.046
Отклонение,	1.38	6.52	6.52	2.27	7.09

 

Таблица 2.4.                                                  Аналоги ускорений

Величина				, м	, м
Графически	0.106	0.26	0.26	0.06	0.0627
Аналитически	0.113	0.265	0.265	-0.052	-0.07
Отклонение,	6	1.88	1.88	15.3	10
Графически	0.130	0.309	0.309	0.011	0.06
Аналитически	0.110	0.309	0.309	0.0152	0.0658
Отклонение,	18	0	0	23	8