Анализ и синтез механизма зубострогального станка для нарезания конических колес, страница 2

1.3.8.  Данный механизм имеет простую структуру, является сложным и однотипным. Он состоит из одного простого механизма – кривошипа (рис. 1.3. а)) и двух структурных групп (рис. 1.3. б)), обладающих нулевой подвижностью.

1.3.9.  Определяем подвижность всего механизма. Исследуемый механизм существует в трехподвижном пространстве, в котором разрешены следующие простейшие движения – два поступательных x иy вдоль соответствующих осей и одно вращательное движение  вокруг оси z.

Подвижность механизма определяется согласно  (1.1). По формуле Чебышева подвижность простого механизма равна 1 (1.2).

                                                              (1.2)

В станке число звеньев n= 5, P₁=7, P₂=0. Тогда .

1.3.10. Согласно определению, группой Ассура называется линейная цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающаяся на более простые цепи, обладающие также нулевой степенью свободы. Классификация по Артоболевскому структурных групп Ассура приведена в таблице 1.4.

Таблица 1.4.                                      Классификация структурных групп

2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

Кинематический анализ любого механизма проводят двумя методами – графическим и аналитическим. Полученные результаты сравнивают между собой. Погрешность расчетов должна составлять не более 5 – 7 %.

На первом этапе исследования закон движения начального звена неизвестен. Он определится в ходе решения. Поэтому при предварительном кинематическом анализе механизма вместо скоростей и ускорений используются их аналоги, которые не зависят от времени, а являются функциями обобщенной координаты.

2.1. Кинематическое исследование механизмов

Аналитический метод исследования механизма заключается в том, что линейные и угловые координаты, скорости и ускорения точек звеньев механизма определяются в виде аналитических выражений.

       Исходными данными для проведения кинематического анализа являются: структурная схема механизма, изображающая механизм в любом положении, размеры звеньев, заданные положения обобщенных координат механизма, законы движения обобщенных координат механизма во времени.

2.2. Метод решений

       Для решения поставленной задачи воспользуемся методом замкнутых векторных контуров. Для этого необходимо поступать следующим образом:

       2.1. Рисуем структурную схему механизма в промежуточном положении.

       2.2  Выбираем координатную систему. Обычно начало системы координат совмещают со стойкой первого звена.

       2.3. В соответствии с методом все звенья механизма заменяем векторами произвольного направления. Положение этих векторов в пространстве характеризуется углами, величина которых определяется при мысленном повороте оси x системы координат против часовой стрелки. Правило иллюстрируется рис. 2.1.

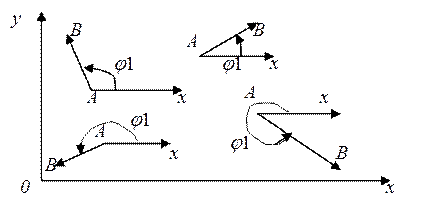
Рис.1.2. Определение углов направления векторов

       2.4. Полученные векторы объединяем между собой так, чтобы получились замкнутые контуры. При этом одни и те же векторы могут входить в несколько контуров одновременно, но так, чтобы один контур имел в своем составе не более двух неизвестных величин.

       2.5. Составляем векторные уравнения замкнутости полученных контуров. Если направление вектора совпадает с выбранным направлением обхода, то он в уравнении записывается со знаком плюс, в противном случае – со знаком минус.

       2.6. Проецируем векторные уравнения замкнутости на оси координат x и y и получим базовые системы уравнений для расчета кинематических характеристик звеньев. 

2.3. Решение