Анализ и синтез механизма зубострогального станка для нарезания конических колес, страница 4

            Рассматриваем второй расчетный угол, величина которого . Аналогичным образом определяем значения всех неизвестных и получаем в итоге таблицу 2.2.

Таблица 2.2.                          Результаты расчета звеньев

            2.3.1. Определение аналогов скоростей и ускорений аналитическим методом

            Кинематические свойства механизма, когда закон движения начального звена еще неизвестен, находят с помощью кинематических характеристик, которые называются аналогами скоростей и ускорений и которые не зависят от времени, являясь функциями обобщенной координаты.

            Аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, поэтому принимаем .

Аналитическое определение аналогов скоростей и ускорений основано на дифференцировании по обобщенной координате уравнений (2.3) и (2.5). Отсюда получим следующие системы:

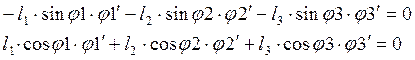                                                           (2.17)

            Из системы (2.5):

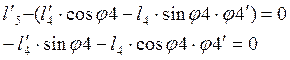                                                                           (2.18)

            Решая (2.17), получим значения :

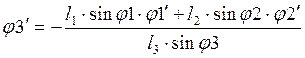
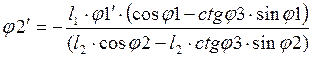                      (2.19)

            Из системы (2.18) получим:

                                               (2.20)

Аналоги ускорений получим, дифференцируя системы (2.17)-(2.19) по обобщенной координате и принимая .

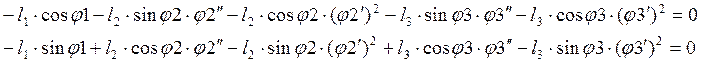            (2.21)

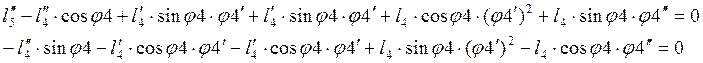(2.22)

Выражаем из данных систем неизвестные, считаем их значения и сравниваем с графическим методом.

Из системы (2.21) получим:

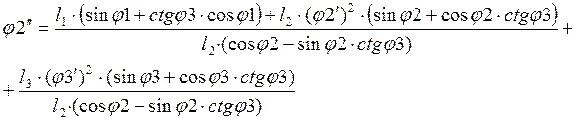                          (2.23)

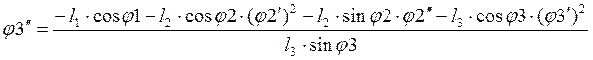                       (2.24)

            Из системы (2.22) получим такие выражения:

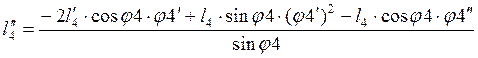                                              (2.25)

                             (2.26)

           Аналитически неизвестные величины (скорости и ускорения) были получены с помощью Mathcad (приложение 2).

           2.3.2. Определение аналогов скоростей и ускорений графическим методом

Графически угловые и линейные скорости определяются таким образом:

Ели начальное звено совершает вращательное движение, то скорость любой его точки определяется так: , где - скорость точки A, - кратчайшее расстояние от оси вращения до точки A, - угловая скорость звена 1. Скорость точки A перпендикулярна прямой AO и на плане скоростей изображается вектором , модуль которого определяется

так: 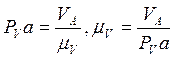. Здесь - масштабный коэффициент, - полюс плана скоростей, выбираемый в произвольном месте чертежа.

Далее определяем скорость точки B. Данная точка находится в сложном движении относительно точек A и D. Поэтому абсолютная скорость точки определится как векторная сумма . В этом уравнении одной чертой подчеркнуты слагаемые, для которых известны направления, а модули подлежат определению, двумя чертами подчеркнуто слагаемое, для которого известны и модуль, и направление. Здесь  направляется перпендикулярно звену AO, - перпендикулярно AB, а абсолютная скорость точки B – перпендикулярно CD, поскольку точка B движется относительно точки C. Модуль скорости определяются по формуле: . Но угловая скорость второго звена нам неизвестна, поэтому записанное выше уравнение решаем графически.