Анализ и синтез механизма зубострогального станка для нарезания конических колес, страница 3

       Применим к заданному механизму метод замкнутых векторных контуров (см. рис.1.1).

       Структурную схему механизма располагаем в прямоугольной системе координат, начало которой помещено в точку O. Со звеньями механизма связываем векторы так, чтобы они образовали замкнутый контур (рис. 2.2).

Рис.2.2. Метод замкнутых контуров

В итоге получили три замкнутых контура: OABC, OEDC, OFE. При образовании контура необходимо учитывать то, что в него не должно входить более 2 неизвестных. Углы, определяющие положения векторов, отсчитываются против хода часовой стрелки от положительного направления оси x.

Запишем уравнение замкнутости первого и последующих контуров. Для этого выбираем направление обхода данного контура. Пусть направление обхода будет совпадать с направлением движения часовой стрелки. Векторы, направление которых совпадает с направлением обхода, записываются со знаком плюс, в противном случае – со знаком минус (2.1):

OABC                                     OEDC                                     OFE

                                                       (2.1)

Уравнениям (2.1) соответствуют 6 скалярных уравнений – проекций на оси координат x и y для каждого контура соответственно.

Рассмотрим контур OABC.

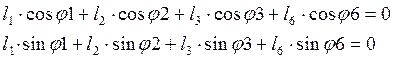                                                   (2.2)

С учетом  получим систему уравнений вида 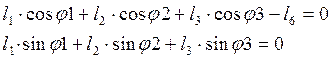(2.3):

                                                                (2.3)

КонтурOEDС.

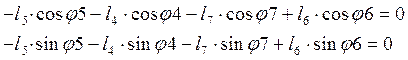                                                       (2.4)

Учитывая , получим 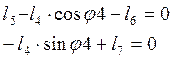(2.5):

                                                                                                                  (2.5)

       Контур OFE.

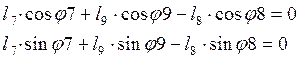                                                                                         (2.6)

 

Учитывая , получим:

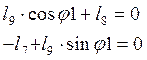                                                                                                     (2.7)

Для простоты решения разбиваем контуры на более простые, в которых будет только две неизвестных. Тогда:

Данный контур разбиваем на два более простых, вводя дополнительный вектор l₁₀, который характеризуется углом . Рассматриваем контур OAC. В проекциях на оси координат получим уравнения:

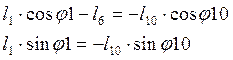                                  (2.8)

Рис. 2.3. Контур ОАВС

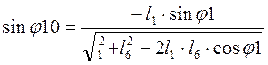Система уравнений (2.8) была получена с учетом равенства . Отсюда выражаем неизвестные  (2.9).

                          (2.9)

Далее аналогично для контура OBC (2.10).

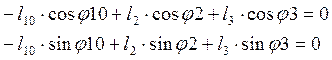                                                                                     (2.10)

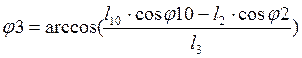
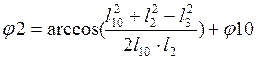                            (2.11)

Формула (2.11) представляет собой выражение неизвестных .

Рассматриваем контур OEDC (рис.2.4). В данном контуре неизвестные . Угол  выражается через уже найденный угол  - формула (2.12).

                              (2.12)

Система уравнений, полученная в результате проецирования векторов на оси координат, имеет вид (2.13)

Рис. 2.4.Контур OEDC 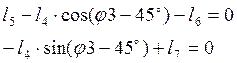                                            (2.13)                                                   

Решая систему (2.13), получим (2.14):

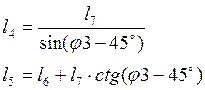                                                                                                   (2.14)

Далее проделываем аналогичную операцию с контуром OFE.

 

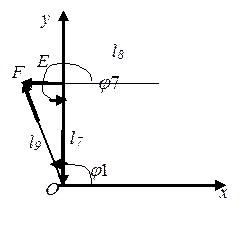Проецируя векторы на оси координат, получим систему уравнений (2.15). Затем, решая её, найдем неизвестные  (2.16).

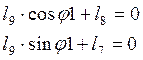                   (2.15)

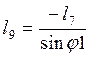
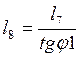                                  (2.16)

Рис.2.5. Контур OFE

Таким образом, все неизвестные определены. Теперь необходимо проверить соответствие неизвестных, найденных аналитически, с неизвестными, определенными с плана положений.

Для первого расчетного угла при  находим из решения системы уравнений (2.2) в MathCad  (приложение 1). Значение угла  определяем через найденные величины по формуле (2.12), неизвестную длину  определяем из (2.14).

В итоге получим таблицу 2.1, в которой приведены значения неизвестных, полученные разными методами – графическим и аналитическим.

Таблица 2.1.                          Результаты расчета звеньев