Параметрический синтез системы автоматического регулирования температуры теплоносителя, страница 4

По результатам заполнения таблицы вычисляются интегральные площади по формулам:

1) F₁ = t ;                                 

    F₁= ;

2) F₂ =;

F₂ = ;

3) F₃ = ;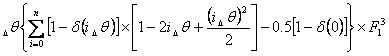        

            F₃ = .

В результате аппроксимации получаем передаточную функцию третьего порядка вида:

                           ,

где   а₁ = F₁ = 0.363;     a₂ = F₂ = 0.0494;     a₃ = F₃ = 0.0028.

Тогда:       

По результатам расчетов также строим расчетную переходную характеристику, сравниваем ее с экспериментальной и находим ошибку аппроксимации, см. рисунки 2.2.1 и 2.2.2, а также таблицу 2.2.2:

 

Рисунок 2.2.1 - Расчетная переходная характеристика объекта

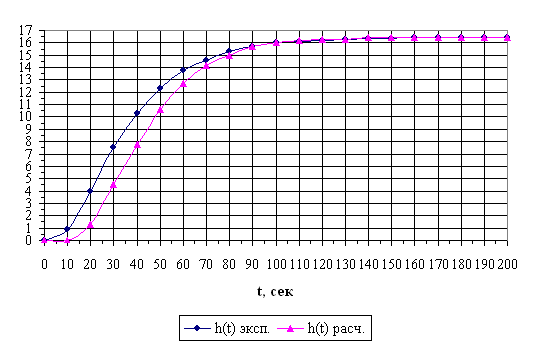
Рисунок 2.2.2 - Совмещение расчетной и экспериментальной переходных характеристик

Таблица 2.2.2 - Расчет ошибки аппроксимации.

t, сек	h(t) эксп.	h(t) расч.	Δ
0	0	0	0
10	0,9	0	5,487805
20	4	1,3	16,46341
30	7,5	4,5	18,29268
40	10,3	7,8	15,2439
50	12,3	10,6	10,36585
60	13,8	12,7	6,707317
70	14,57	14,2	2,256098
80	15,3	15	1,829268
90	15,7	15,7	0
100	16	16	0
110	16,1	16,2	-0,60976
120	16,2	16,25	-0,30488
130	16,3	16,3	0
140	16,35	16,4	-0,30488
150	16,37	16,4	-0,18293
160	16,4	16,4	0
170	16,4	16,4	0
180	16,4	16,4	0
190	16,4	16,4	0
200	16,4	16,4	0