Математика \ Дискретная математика

Нелинейные системы, передаточные функции - задачи для подготовки к Госэкзаменам, страница 5

 — спектральная плотность

Замена p à jω

 Отсюда:

2)   

ЗАДАЧА 14. Передаточная функция системы имеет вид:      где k = 30, Т1 = 0.025, Т2 = 0.2. С помощью логарифмических частотных характеристик определить критическое время запаздывания tкр.

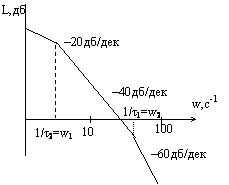k=30, Т1=0.025, Т2=0.2. С помощью ЛЧХ определить критическое время запаздывания  tкр,  ЛАЧХ и ЛФЧХ.

Решение: асимптотическая ЛАЧХ системы:

частота среза разомкнутой системы wс=12.6 c-1. Фазовая частотная характеристика при частоте w=wc и критическом времени запаздывания tк должна пересекать линию j=-p, поэтому

j(wc)=–p/2–arctg wc*T1- arctg wc*T2 –wc*tк=–pÞtк=(p/2–arctg wc*T1- arctg wc*T2)/ wc

tк=4.8*10-2c

ЗАДАЧА 15. С помощью критерия Михайлова по методу перемежаемости корней определить устойчивость замкнутой системы, если передаточная функция разомкнутой системы имеет вид:

, где k = 20, , Т1 = 1, Т2 = 5, Т3 = 0.025.

Определим передаточную функцию замкнутой системы:

 Отсюда характеристическое уравнение системы равно:

Замена p à jω

Разделяем вещественную и мнимую части:

Подставив заданные значения получим:

Для устойчивости системы необходимо и достаточно, чтобы корни мнимой и вещественной частей его характеристического уравнения были положительными, вещественными и чередовались.

Так как условие не выполняется то делаем вывод, что система неустойчива.

ЗАДАЧА 16. Определить разности 1, 2, 3–го порядков для решетчатой функции:

ЗАДАЧА 17. Составить  дифференциальное  уравнение электрической цепи относительно выходного Uвых и входного Uвх напряжений, получить передаточную функцию и построить частотные характеристики в общем виде.

Решение: составим д.у. относительно вх. и вых. сигналов согласно 2 закону Кирхгофа.

Uвх=IR+Uвых (1) выражаем I ч/з Uвых I=c(dUвых/dt)(2), подставляем (2) в (1): Uвх=СR(dUвых/dt)+ Uвых(3) т.к. Т= СR, то выражение (3) примет вид

Т(dUвых/dt)+ Uвых =Uвх(4), запишем его в операторной форме Тр Uвых(р)+ Uвых(р)= Uвх(р)(5)

из выражения (5) находим передаточную ф-ю схемы:

 W(р)= Uвых/Uвх=1/(Тр+1)

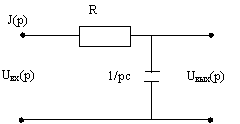Если параметры данной схемы записать в операторной форме, т.е. Uвх»Uвх(р), Uвых»Uвых(р),

Скачать файл