Составив ПФ для замкнутой системы, найдем характеристическое уравнение:
Для устойчивости системы достаточно:
и 
Таким образом для устойчивости системы достаточно:
и 
Система
наход-ся на гр. Устойчивости если глав. определитель 
Отсюда
найдем kкр: 
не подходит 
(ответ)
ЗАДАЧА 7. Характеристическое
уравнение импульсной системы имеет вид: 
Получить условие устойчивости системы, используя дискретный критерий Рауса-Гурвица.
Произведем
замену 
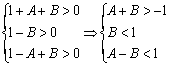— условие устойчивости
ЗАДАЧА 8. Найти оптимальный
закон управления, который удовлетворяет уравнению объекта 
и обращает в минимум функционал 
при ограничении на управляющее
воздействие 
Оптимизация по быстродействию
Вводим замену
à С учетом введенных
обозначений
(*)
Функционал данной задачи I не зависит от
управляющего воздействия u, поэтому в систему уравнений (*) можно не
включать Ур-ия которые характеризуют текущее значение функционала: 
— не включается в систему. Составим
ф-цию Гамильтона:
Необходимо чтобы выполнялось условие: 
Отсюда: 
То
есть оптим. з. управления: 
Определим вспом. ф-ции φ1 и φ2:
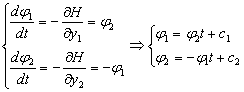Таким образом, оптимальный з.
управления: 
ЗАДАЧА 9. Найти передаточную функцию электрической цепи относительно выходного Uвых и входного Uвх напряжений, построить АЧХ в общем виде.
Запишем выражение для передаточной функции:
, 
,
=> 
где 
,
,
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
; 
;
;