Нелинейные системы, передаточные функции - задачи для подготовки к Госэкзаменам, страница 4

ЗАДАЧА 10. Определить запасы устойчивости системы по модулю и фазе:

Решение: передаточная функция разомкнутой системы примет вид :

Строим ЛАЧХ и ЛФЧХ для чего определяем сопрягающие частоты:

  ,   , 20 lg k=20 lg 200 =46

  ,  w_СР=70 c^-1

w	0	5	10	20	30	40	50	60	70	80
j(w)	0	-46,5	-82,9	-130	-159	-178	-191,9	-202	-210	-217

Вывод: т.к. ЛАЧХ пересекает ось lg w позже , чем ЛФЧХ переходит значение -p , то замкнутая система неустойчива , т.е. запаса устойчивости нет ни по фазе ни по модулю

ЗАДАЧА 11. Замкнутая нелинейная система содержит:

- линейную часть с передаточной функцией:   

                - нелинейное звено со статической характеристикой:                                      

Требуется определить параметры автоколебательного режима.

Составим характеристическое уравнение системы:

Замена p à jω

Разделяем вещественную и мнимую части:

→ — амплитуда авток. режима

ЗАДАЧА 12. Система описывается  дифференциальным  уравнением вида:

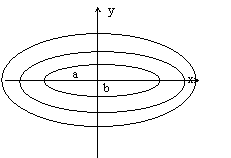Построить фазовую траекторию и сделать вывод о характере  колебаний.

Решение : 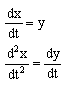  , 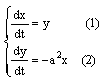 Разделим (2) на (1)  :     =>

     ,       ,     ,    ,  b=c

Фазовые траектории соответствуют  эллипсам (в зависимости от начальных условий) .

ЗАДАЧА 13. Определить спектральную плотность случайного сигнала при прохождении его через: - идеальное дифференцирующее звено с коэффициентом передачи k = 1 с; - реальное интегрирующее звено.

1)  — идеальное диф. звено с коэф. передачи k = 1 c.