Нелинейные системы, передаточные функции - задачи для подготовки к Госэкзаменам, страница 2

Строим кривую Михайлова :

Вывод: Система в замкнутом  состоянии устойчива, т.к. кривая Михайлова проходит последовательно число квадрантов =3 , т.е. совпадающее с наивысшей степенью исходного уравнения.

ЗАДАЧА 4. Оценить время регулирования, если известна передаточная функция разомкнутой системы:

Определим время регулирования из соотношения: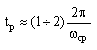

w_ср – точка пересечения  ЛАЧХ с осью абцисс

Для построения ЛЧХ найдем сопрягающие частоты :

1)  500/p: -20 дБ/дек, ω₁ = 1, lg ω₁ = 0 , 20 lg 500 =53,98;

2)  1+0.05p: -20 дБ/дек,, lg ω₂ = 1,30

3)        1+0.017p: +20 дБ/дек,, lg ω₃ = 1,77

4)         1+0.0025p:,  lg ω₃ = 2,60

5)         1+0.001p:   ,  lg ω₄ = 3

lg w_ср = 2,2   ,  w_ср =10^2,2 =158 с^-1

Для полной уверенности  можно проверить  устойчива ли система на этой частоте. Найдем ЛФЧХ , как

Подставляя  значение получим :j(w_ср)= -134 ⁰ > -180 ⁰ => система устойчива

ЗАДАЧА 5. Уравнение системы в разомкнутом состоянии имеет вид:

Построить логарифмические частотные характеристики и сделать вывод об  устойчивости замкнутой системы.

Решение: для определения передаточной функции запишем уравнение САР в операторной форме:

;

Передаточная ф-я системы:

Разложим полином второй степени по итерационным формулам: b₀= 0,004  ; b₁=0,4 ;  ;  Следовательно, полином разложится в виде:

 ;  

Передаточная функция: Строим логарифмические характеристики:, , =2, 20 lg k = 20 lg 1=0

                                              

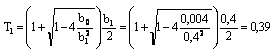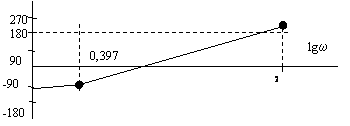ЛФЧХ пересекает линию j=-180 ⁰ при  отрицательных значениях асимптотической ЛАЧХ . Следовательно , замкнутая система устойчива .

ЗАДАЧА 6. Передаточная функция разомкнутой системы имеет вид

С помощью критерия Рауса-Гурвица получить условие устойчивости замкнутой  системы и определить значение коэффициента передачи k_кр, при котором система окажется на границе устойчивости.