Редуктор одноступенчатый горизонтальный привода ленточного конвейера, страница 4

Межосевое расстояние рассчитываем по формуле [1,с.21]:

a_w= K_a*( U₁+1)*,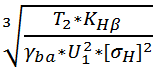

где  K_a – коэффициент межосевого расстояния,

        - коэффициент неравномерности распределения нагрузки по длине контактной линии, полученной в результате погрешностей в зацеплении и деформации зубьев,

        - коэффициент ширины колеса по межосевому расстоянию,

       – крутящий момент на тихоходном валу, Н*мм.

       K_a=49,5 – для прямозубых колёс [1,с.20]

=1+(2*/S)2,0 [1, с.20],

где  - коэффициент ширины колеса по делительному диаметру,

      S – индекс схемы проектируемого редуктора.

=0,5**(U₁+1).

Согласно рекомендации [1,с.15] принимаем =0,4, тогда

=0,5*0,4*(3,3+1)=0,86.

По рекомендации [1,с.21, таблица 2.3] значение S принимаем равным 8 (колёса на валах расположены симметрично), тогда:

=1+2*0,86/8=1,2,

T₂=241Н*м (см. п.р.1.11).

Найденные значения коэффициентов подставляем в формулу  

a_w= 49,5*( 3,3+1)*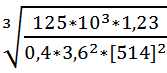=106,4 мм.

Полученное значение округляем в большую сторону по рекомендации [1,с.481, таблица 19.1], т.е. принимаем a_w=110мм.

2.4 Расчёт предварительных основных размеров колеса

=2* a_w* U₁/( U₁+1)  [1,с.21],

где   - делительный диаметр, мм

=2*110*3,3/(3,3+1)=168,8 мм.

Ширина колеса определяется по формуле [1,с.22]

=* a_w,

=0,4*110=44мм.

Принимаем по [1,с.481, таблица 19.1] =45 мм.

Ширина шестерни определяется по формуле [1,с.24]:

/==1,08,

=1,08*=1,08*45=48,6 мм.

Принимаем по [1,с.481, таблица 19.1] =50 мм.

2.5 Расчёт и выбор по СТ СЭВ модуля передачи

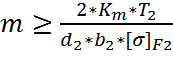  [1,с.22],

где   - коэффициент модуля, для прямозубых колёс – 6,8.

=2*6,8*125*10³/(168,8*45*256)=0,87 мм.

Принимаем по рекомендации  модуль передачи =1 мм.

2.6 Определение суммарного числа зубьев

Суммарное число зубьев для прямозубой передачи по [1,с.22]:

=,

=2*110/1=220.

Если полученное значение не является целым числом, то округляем его в меньшую сторону до целого числа.

Принимаем =220.

2.7 Определение числа зубьев шестерни и колеса

Число зубьев шестерни рассчитываем по [1,с.22]:

=,

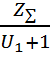=220/(3,3+1)=51,2, принимаем =51.

Число зубьев колеса по [1,с.23]:

=-,

=220-51=169.

2.8 Определение фактического передаточного числа

=/ [1,с.23],

=169/51=3,31.

Отклонение от передаточного отношения

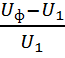=*100% [1,с.23]

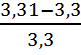=*100%=0,003%.

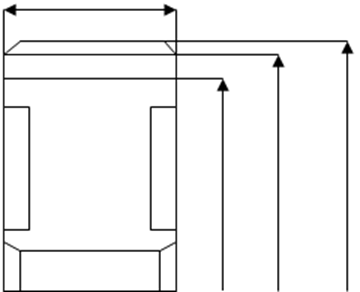
2.9 Определение геометрических размеров колеса

                                                                    

 

                                          Ǿ       Ǿ                              

 

Рисунок 1 – Основные размеры зубчатого колеса

Делительный диаметр шестерни по [1,с.23]:

=*m

=51*1=51 мм.

Делительный диаметр колеса по [1,с.23]:

=2*-,

=2*110-51=169мм.

Диаметры окружностей вершин и впадин зубьев колеса и шестерни по [1,с.23]:

=+2m,

=51+2*1=53 мм,

=-2,5*m,

=51-2,5*1=48,5 мм,

=+2m,

=169 +2*1=171мм,

=-2,5*m,

=169-2,5*1=166,5 мм.

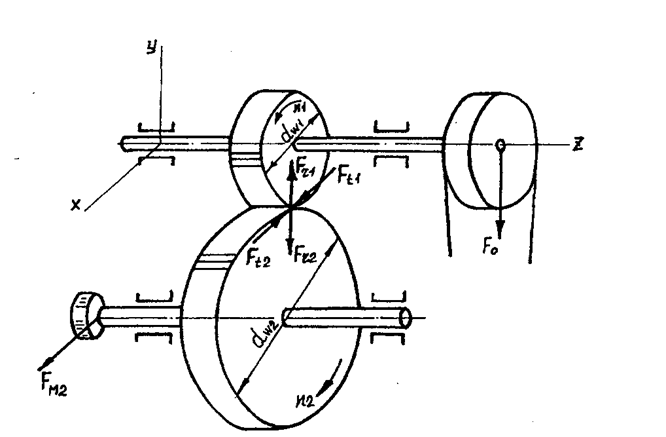
2.10 Определение усилий в зацеплении

Окружная сила по [1,с.24]:

=2*/,

=2**10³/=1479,3 Н.

Радиальная сила по [1,с.24]:

=*tg.

В соответствии с рекомендацией [1,с.24] для стандартного угла

=20⁰,

tg=0,364.

=*0,364=538,5 Н.

=0 (передача прямозубая).

2.11 Проверка зубьев колёс по напряжениям изгиба

Действительное напряжение изгиба в зубьях колёса по [1,с.15]:

=*****/(*m),

где   - коэффициент, учитывающий распределение нагрузки между зубьями,

        - коэффициент, учитывающий угол наклона зуба,

        - коэффициент, учитывающий распределение нагрузки по длине зуба,

        - коэффициент, учитывающий окружную скорость колёс,

        - коэффициент, учитывающий форму зуба.

Определяем окружную скорость по  [1,с.25]:

 

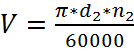
=169 мм (см. п.р.2.9),

=214,8 об/мин (см. п.р.1.10),

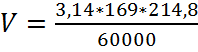=1,9 м/с,

=1479,3  (см. п.р.2.10),