Оптимизация развития электроэнергетических систем, страница 2

Введение

Значительная часть исследований в электроэнергетике, как и в других отраслях техники, составляют так называемые оптимизационные задачи. Задачей оптимизации называется экстремальная задача, где при решении заданной системы уравнений и накладываемых ограничений необходимо определить экстремум целевой функции. При этом целевую функцию часть называют критерием. В многоэкстремальных целевых функциях присутствует множество локальных критериев, наибольший из которых глобальный.

Для ЭЭС характерным оптимизационными задачами являются:

1.  Управление нормальными установившимися режимами ЭЭС.

2.  Планирование разбития ЭЭС на разную временную перспективу.

В данном курсовом проекте рассматривается вторая задача.

Необходимо выполнить оптимизацию структуры генерирующих мощностей (СГМ) электроэнергетической системы, состоящей из трех объединенных энергосистем (ОЭС), связанных межсистемными связями. А так же выбрать оптимальную конфигурацию электроэнергетической сети для системы из восьми подстанций.

Формирование модели выбора структуры генерирующих мощностей заключается в линейной экономико-математической задачи модели выбора структуры генерирующих мощностей, в расчете коэффициентов уравнений ограничений и целевой функции и в выборе оптимальной структуры симплекс-метода.

Выбор структуры генерирующих мощностей на ЭВМ включает в себя работу с программой OSGM, которая по начальным данным, находящихся в задании на курсовой проект, составляет оптимальную структуру генерирующих мощностей и ее анализ.

Выбор оптимальной конфигурации электрической сети осуществляется при помощи программы «OPTIMUM», а также производится расчет перетоков мощности, выбор напряжения, сечения проводов трансформаторов, принципиальной схемы

          I. Формирование моделей выбора структуры генерирующих мощностей

1.1 Линейная экономико-математическая модель выбора СГМ.

Задачи выбора СГМ:

В общем виде задача выбора СГМ формулируется следующим образом: определить значение суммарных мощностей различных типов электростанций, а также пропускных способностей Эл.перередач, обеспечивающих минимум приведенных затрат по энерго системе. С учетом существующей структуры и система образующей сети, динамики роста нагрузок и электро потребления, набора возможных сооружений типов электро станций и их технико экономических характеристик.

Полный учет особенностей энерго системы требует разработки нелинейной модели оптимизации СГМ: дискретность ввода энерго обьектов; динамический характер развития энерго систем. Однако опят расчетов показал целесообразность сведения этой задачи к общей задаче линейного программирования.

Задача линейного программирования в общем виде.

         Требуется найти min целевой функции Ф:

           

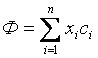
при выполнении системы ограничений:

                

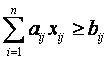
            x_i – оптимизируемые параметры

c_i – константы функционала, соответствующие в экономических задачах удельным затратам на единицу затрат параметра

a_ij – константы, используемые для описания с помощью ограничений технологических и экономических связей между объектами

2

В нашем случае линейная экономико-математическая модель выбора СГМ выглядит следующим образом: для каждого узла е в дополнение к мощности существующей электростанции j-го типа использующие топливо вида i – P_эсеij  должна быть определена  величина вновь вводимой мощности Х_eij , так же перетоки мощности между системами X_ee’ и X_e’e . За критерий оптимальности принимается минимум суммарных приведенных затрат на развитие электростанции и линий электропередач.