Идентификация объекта управления, страница 3

;             

                                    

                                       
Строим переходную характеристику замкнутой системы автоматического регулирования:

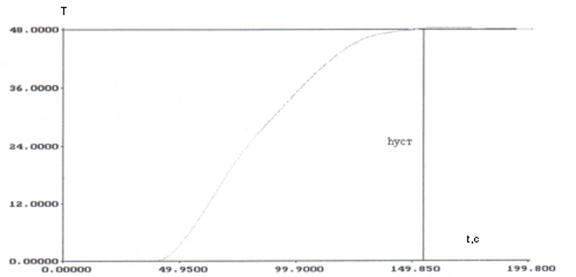
Рисунок 13. Переходная характеристика замкнутой САР с настройками регулятора, полученными методом номограмм.

5.1. Оценка качества регулирования (для метода номограмм)

Оценим качество переходного процесса замкнутой САР для метода номограмм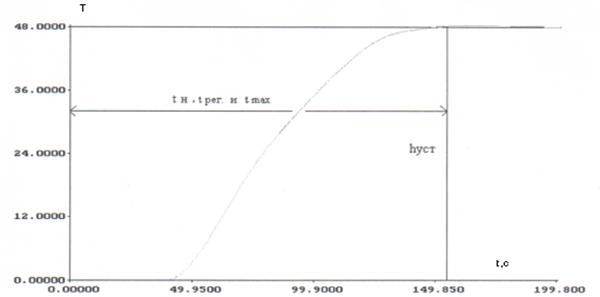

Рисунок 14. Переходная характеристика замкнутой САР (метод номограмм).

4.2. Метод расширенных АФЧХ

Для условия устойчивости необходимо и достаточно, чтобы корни характеристического уравнения имели отрицательные вещественные части.

Если все корни характеристического уравнения лежат левее некоторой прямой, проведенной в левой полуплоскости параллельно мнимой оси на расстоянии g от нее, то система обладает некоторой степенью устойчивости. Величина g характеризующая интенсивность затухающего процесса, численно равна абсолютному значению действительной части корня характеристического уравнения, это называется степенью устойчивости переходного процесса. Степень колебательности переходного процесса m характеризует затухание его колебательных составляющих и численно равна абсолютному значению отношения действительной части к коэффициенту при мнимой части корня характеристического уравнения с наименьшим абсолютным значением этого отношения.

p=-mw+jw

Степенью затухания \jf называют отношение разности двух соседних амплитуд к первой из них. Ее можно выразить через степень колебательности процесса:

,

где 2πm - логарифмический декремент затухания колебаний.

tg γ = m, т.е. получаем, что γ=arctg m

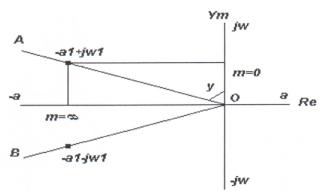
Степень затухания рассматриваемой составляющей процесса будет определяться значением тангенса этого угла. Если корень характеристического уравнения этой системы будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания  будет постоянной.

Выражение передаточной функции звеньев, для которых р находится на линии АОВ, называется расширенной АФЧХ:

Если m=0, то РАФЧХ совпадает с линией АОВ и совмещается с мнимой осью, следовательно, АОВ - мнимая ось, а система находится на границе устойчивости. При расчете системы используется соотношение:

 

Если корень характеристического уравнения системы будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания будет одна и та же.