![]() .
.
![]() ;
; ![]()
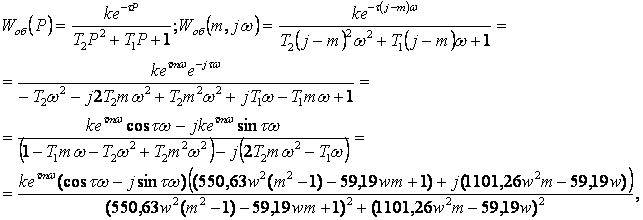
![]() ,
,
![]()
![]()

Решая систему уравнений, находим выражения для С0 и С1.
![]()
![]()
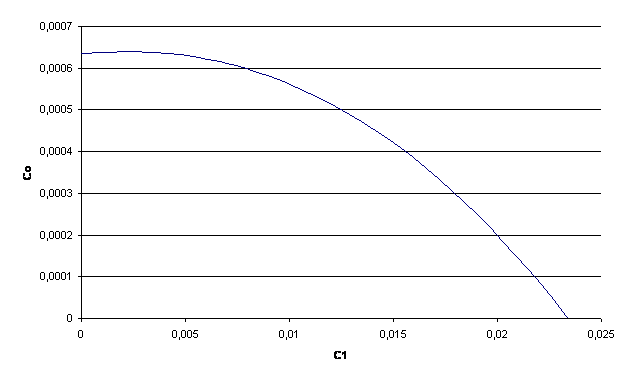
Подставляя различные частоты от 0 до значения, при котором С0 становится отрицательным, строим зависимость С0=f(C1) для m=0,9:
Далее приводятся переходные процессы при настроечных параметрах регулятора:
1.C![]() =0,00054,
=0,00054,![]() =0,010949
=0,010949 ![]() =0,010949,Tи=Kр/C0=20,28 I=111323,1
=0,010949,Tи=Kр/C0=20,28 I=111323,1
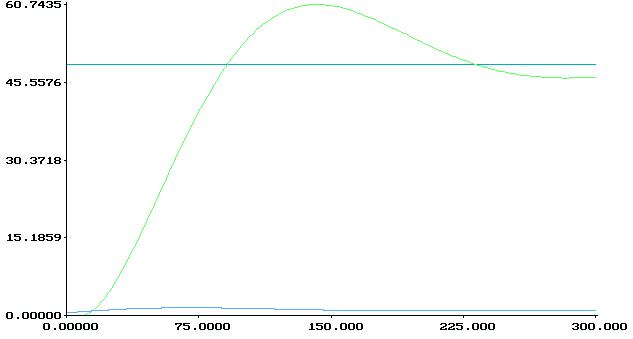
2.C![]() =0,000472,
=0,000472,![]() =0,0134538
=0,0134538![]() =0,0134538,Tи=Kр/C0=28,504
=0,0134538,Tи=Kр/C0=28,504 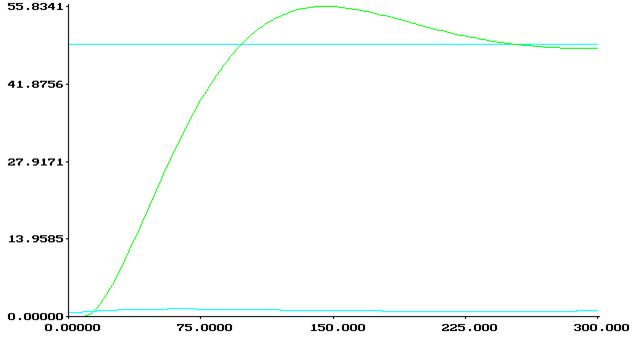
I=102547.8
3. C![]() =0,0003343,
=0,0003343,![]() =0,017191
=0,017191 ![]() =0,017191,Tи=Kр/C0=51,4183
=0,017191,Tи=Kр/C0=51,4183
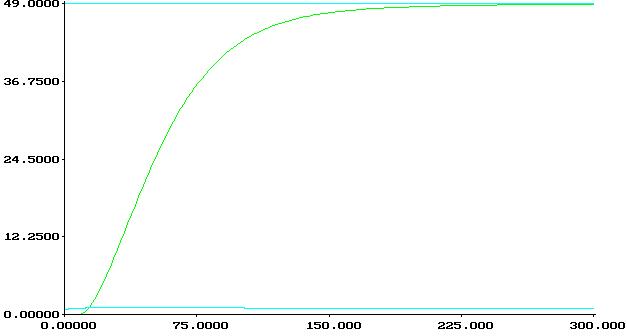
![]() I=99012.04
I=99012.04
4.C![]() =0,000431,
=0,000431,![]() =0,0147008
=0,0147008![]() =0,0147008,Tи=Kр/C0=340108
=0,0147008,Tи=Kр/C0=340108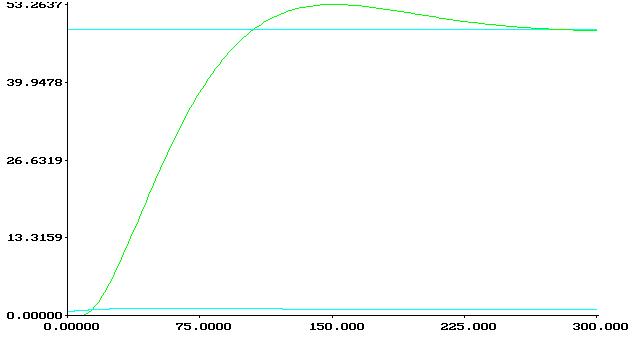
I=99848.96
5.C![]() =0,000218,
=0,000218,![]() =0,0196605
=0,0196605![]() =0,0196605,Tи=Kр/C0=90,186
=0,0196605,Tи=Kр/C0=90,186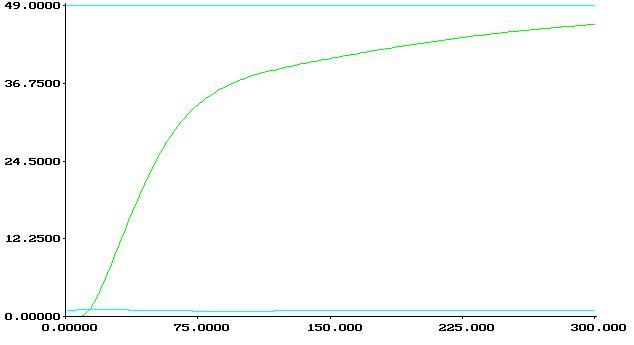
I=109658.2
6.C![]() =0,0000805,
=0,0000805,![]() =0,0221001
=0,0221001![]() =0,0221001,Tи=Kр/C0=274,534
=0,0221001,Tи=Kр/C0=274,534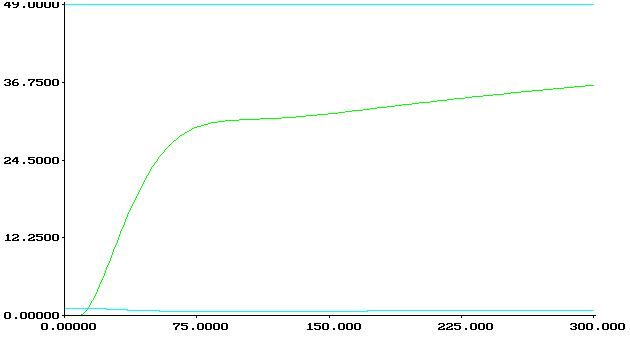
I=154489.8
Как видно из графиков, оптимальным является рис.№3.
Степень затухания процесса определим так:
![]()
![]()
![]()
![]() , где
, где ![]() -
логарифмический декремент затухания.
-
логарифмический декремент затухания.![]()
![]()
![]() 0.996
0.996
6. Интегральная оценка качества переходных процессов.
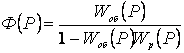 - передаточная функция замкнутой САР.
- передаточная функция замкнутой САР.
Подставляем передаточные функции объекта и регулятора и получаем:
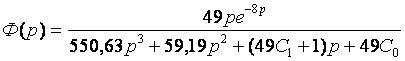
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.