Аппроксимация переходной характеристики объекта апериодическим звеном I порядка с запаздывающим аргументом, страница 6

   Сравнивая 3 метода определения ПФ, выбираем тот, в котором ошибка будет наименьшей. В нашем случае это первый метод, т. к. ошибка в нем наименьшая.  

ПФ по первому методу имеет следующий вид:

.

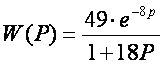В дальнейших расчетах будем использовать именно эту ПФ.

4. Определение переходной характеристики объекта по кривой разгона методом последовательного логарифмирования.

Если переходная характеристика исследуемого объекта является монотонно возрастающей, то её можно представить в виде:

 где i=1…m

Переходная характеристика объекта:

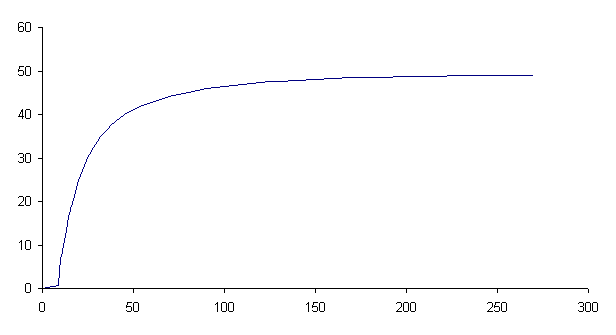
Строим переходную характеристику объекта без запаздывания (t=8 с.)

1.  С₀ определяем из условия Lim h(t);

С₀=h(¥)/Х_вх(t).

Х_вх(t)=1; h(¥)=49; отсюда С₀=49.

2.  Вычислим функцию f₁(t)  и построим зависимость ln|f₁(t)|

Проведём асимптоту к «хвостовой части» и полагаем, что при t® ¥ 

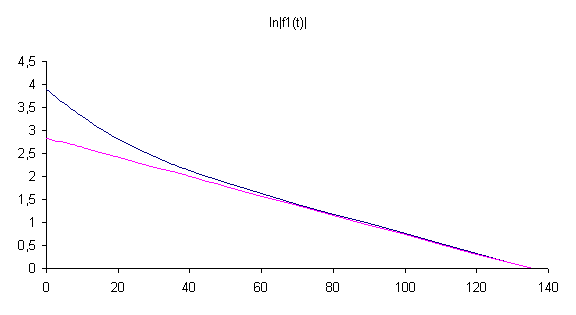
По графику определяем ln|C₁|=2,83

C₁=e^2,83=17,02; t₀=135

a₁=- ln|C₁|/t₀=-0,021;

T₁=1/|a₁|=47,63;

При малых t функция ln|f₁(t)| не совпадает с асимптотой. Найдём «невязку» – функцию f₂(t)=  при следующем неравенстве: 0£t£t₁£t₀

Функция f₂(t) учитывает компоненту , поэтому можно принять, что функция f₂(t)=

3.  Строим график функции ln|f₂(t)|

В данном случае можно принять функцию ln|f₂(t)| за линейную.

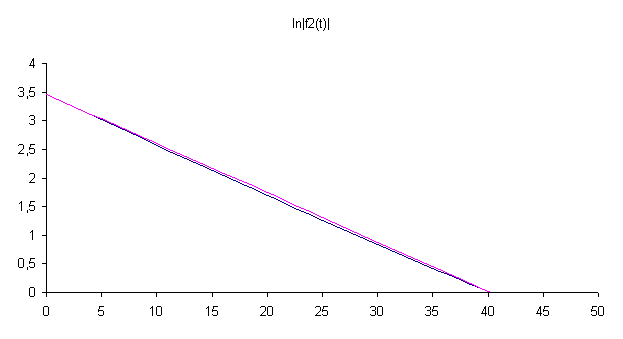По графику определяем ln|C₂|=3,46

C₂=e^3,46=31,84; t₁=40

a₂=- ln|C₂|/t₁=-0,087;

T₂=1/|a₂|=11,56;

В итоге получаем переходную характеристику:

Передаточная функция:

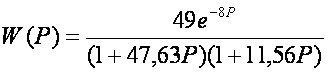
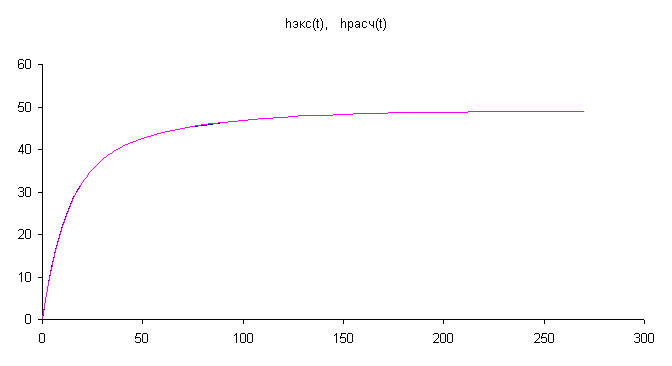
Максимальная ошибка аппроксимации составляет 0,53% при t=10сек, отсюда можно сделать вывод, что данный метод аппроксимации является очень точным и подходит для данной переходной характеристики.

5. Выбор регулятора.

Ввиду того, что отсутствуют данные о допустимых показателях качества  переходного процесса (динамическая ошибка, статическая ошибка, время регулирования), то выбираем ПИ-регулятор.

ПИ-регулятор является астатическим с двумя параметрами настройки:

-  С₁=К_р

-  С₀=К_р/Т_и

Т_и- время изодрома

К_р- коэффициент усиления

При определении настроечных параметров регулятора С0 и С1 будем пользоваться методом расширенных АФЧХ.

При расчете устойчивости системы используется соотношение

W (m, jw)_об*W (m, jw)_р = 1

Передаточная функция системы:

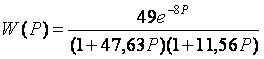
    Произведя в формулах замену  p = w*( j – m), получаем расширенные АФЧХ:

,