Аппроксимация переходной характеристики объекта апериодическим звеном I порядка с запаздывающим аргументом, страница 2

        Максимальная погрешность D = 4,96 % при t = 60 сек. Ошибка аппроксимации должна быть £ 5 %, таким образом условие не выполняется.

2.  Аппроксимация переходной характеристики объекта передаточной

функцией апериодического звена II порядка методом             

 Ольденбурга – Сарториуса.

Пусть экспериментальная переходная характеристика задана в виде графика:

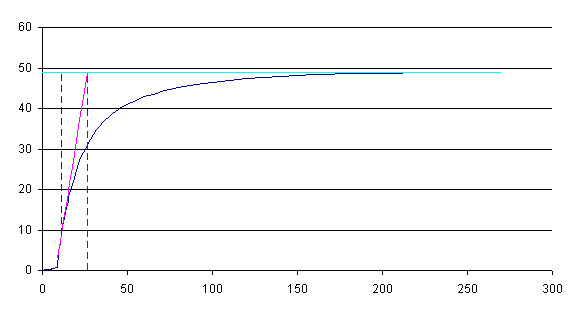
рис.3 Исходная характеристика

Отмечаем точку перегиба на графике и переводим переходную характеристику к нормированному виду, для этого значения всех ее ординат разделить на h_уст

t_р(11;8,54) - точка перегиба;

   К точке перегиба провести касательную до пересечения ее с осью абсцисс и линией установившегося значения выходной величины, находим значения отрезков a,b

a=15,4;  b=18,66;

   Вычисляем отношение a к b

       Пользуясь номограммой откладываем величину m по обеим осям, концы отложенных отрезков соединяем прямой линией. Так как эта прямая лежит ниже кривой L, то поднимаем прямую до пересечения с кривой L в одной точке, отстоящей по оси ординат на расстоянии A и B.

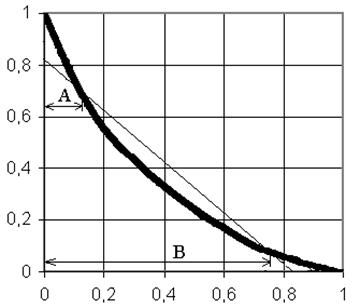
рис.4  Номограмма

 

A=0,126     B=0,757;

  Находим постоянные времени:

  Определяем расчетную точку перегиба:

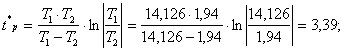
  Находим время запаздывания:

  Передаточная функция будет иметь вид:

 

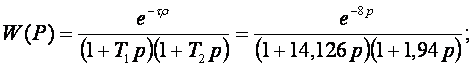
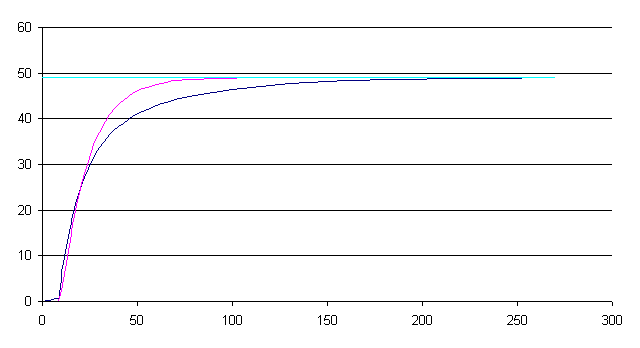
рис. 5 Расчетная  характеристика.

 

t	11	20	36	38	40	45	50	55	60	130	200
h(t)э	8,54	24,75	36,8	37,62	38,35	39,89	41,08	42,06	42,87	47,66	48,69
h(t)р	4,74	24,73	41,2	42,2	43,1	44,86	46,1	46,96	47,57	48,99	49
D %	7,78	0,05	8,93	9,36	9,7	10,15	10,24	10	9,59	2,71	0,63