Аппроксимация переходной характеристики объекта апериодическим звеном I порядка с запаздывающим аргументом, страница 3

          Максимальная погрешность D = 10,24 % при t = 50 сек. Ошибка аппроксимации должна быть £ 5 %, таким образом условие не выполняется.

 

3.  Аппроксимация переходной характеристики объекта методом интегральных площадей

 

Расчет производим методом интегральных площадей в следующей последовательности:

1.  Выделение на экспериментальной кривой участка чистого запаздывания. Оно очень мало и им можно пренебречь.

2.  Выбор Dt интервала разбиения кривой. Значение интервала разбиения определяется, исходя из условия, что на протяжении всего графика функция h(t) в пределах 2Dt мало отличается от прямой. Выбираем  Dt=1 мин.

3.  Строим переходную характеристику в безмерном виде  (кривая разгона) s(t), где    . Для этого значения h(Dt) в конце каждого интервала Dt делим на h_max(t). Получившиеся значения  s(t) заносим в графу 2 таблицы 1. По данным этого столбца заполняем графу 3 и подсчитываем ее сумму.

4.  Определяем площадь F₁ по формуле:

5.  Заполняем графу 4 таблицы 1, где q - безразмерное время и строим       вспомогательную функцию

6.  Заполняем таблицу 2, графы 3 и 5, значения которых выписываем из таблицы подынтегральных функций

7.  Подсчитываем сумму столбца 4, затем столбца 6

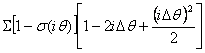
8.  Определение интегральной площади

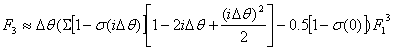
9.  Выбираем структуру передаточной функции. Так как в момент времени t=0, h(0)=h’(t)=h’’(t)=0, то передаточную функцию выбираем вида:

,

где

   Если переходная кривая характеризуется наличием транспортного запаздывания, то порядок расчета следующий:

1. Определяется по графику заданной кривой запаздывание t, как время в течении которого функция h(t) от t=0 до t=t не превышает 0.001h_уст(∞)
2. Определяем передаточную функцию объекта как произведение двух передаточных функций:

,

     соответствующей запаздыванию и W₂(P), соответствующей функции

,

 для которой за начало отсчета принято t=t. Порядок расчета W₂(P)    известен из предыдущего изложения. Тогда передаточная функция примет вид:

Таблица 1

t,мин	s	1 - s	q=t/F1
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270	0 0,120816 0,505102 0,687347 0,782653 0,838367 0,874898 0,90102 0,920816 0,936122 0,948367 0,958367 0,966122 0,972653 0,977755 0,982041 0,98551 0,988163 0,990408 0,992245 0,993673 0,994898 0,996122 0,997143 0,997959 0,998776 0,999388 1	1 0,879184 0,494898 0,312653 0,217347 0,161633 0,125102 0,09898 0,079184 0,063878 0,051633 0,041633 0,033878 0,027347 0,022245 0,017959 0,01449 0,011837 0,009592 0,007755 0,006327 0,005102 0,003878 0,002857 0,002041 0,001224 0,000612 0	0 0,455941 0,911882 1,367824 1,823765 2,279706 2,735647 3,191588 3,64753 4,103471 4,559412 5,015353 5,471294 5,927236 6,383177 6,839118 7,295059 7,751 8,206941 8,662883 9,118824 9,574765 10,03071 10,48665 10,94259 11,39853 11,85447 12,31041