Расчет оборудования для сушки целлюлозы (на примере сушильного цеха № 2 Братского ЛПК), страница 9

          Крутящий момент передаваемый шестерней найден в предыдущих расчетах, М_кр = М = 3011,26 Н ∙ м (формула (3.14)).

          Определяем окружное усилие в зацепление Р₁₀, Н, по формуле

                                        (3.21)

где     d_д – диаметр делительной окружности шестерни, м.

.

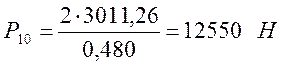          Определяем радиальное усилие в зацеплении Т₁₀, Н, по формуле

                                          (3.22)

где     α – угол зацепления шестерни, град.

Принимаем: α = 20⁰.

.

          Определяем окружное усилие в точке Е Р₁, Н по формуле

,                                               (3.23)

.

Определяем радиальное усилие в точке Е Т₁, Н, по формуле

                                               (3.24)

.

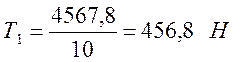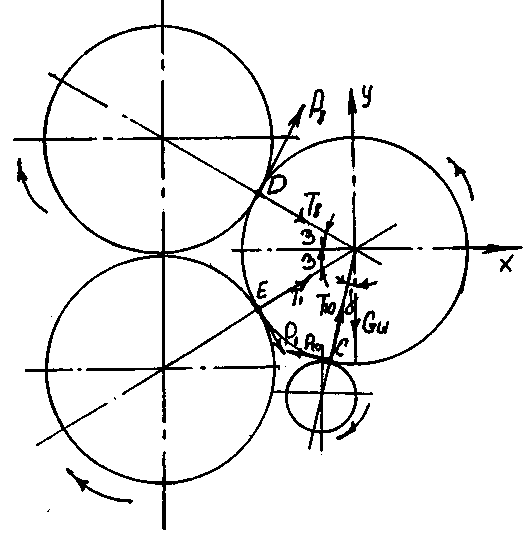
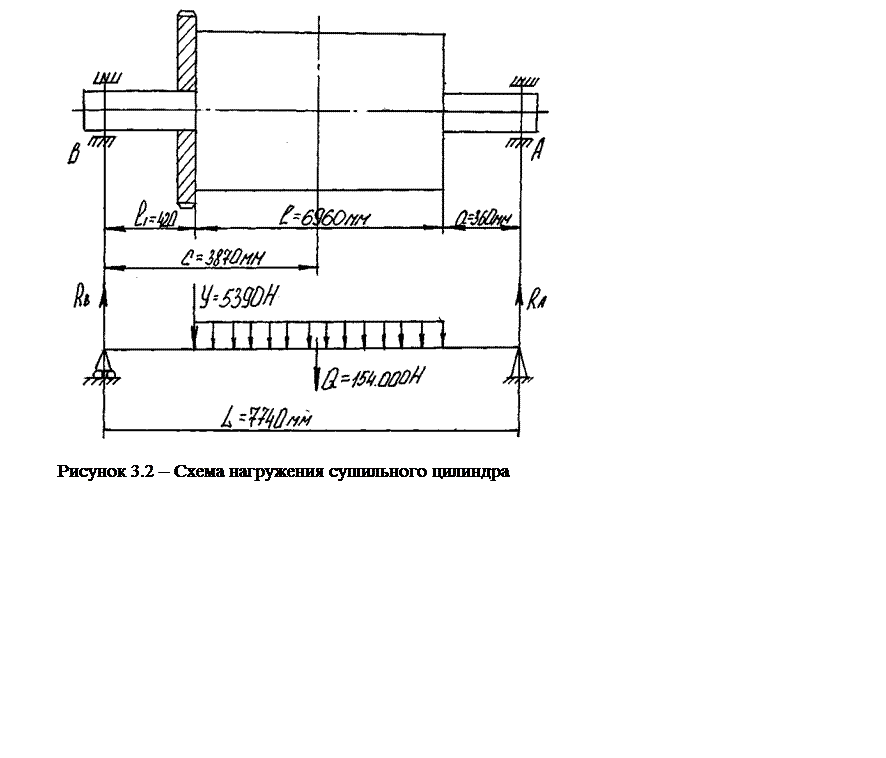
Рисунок 3.1 – Схема нагрузок на шестерни шахматного привода.

          Определяем окружное усилие в точке D P₈, Н, по формуле

                                             (3.25)

.

          Определяем радиальное усилие в точке D  T₈, Н, по формуле

                                              (3.26)

.

          Проводим сумму проекций на ось Y, P_Y, Н, по формуле

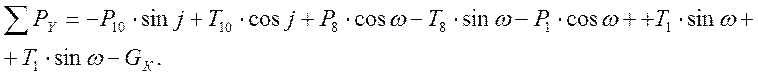      (3.27)

          Принимаем: j = 11⁰; ω = 31⁰24^/.

Аналогично проектируем все силы на ось Х - , по формуле

         ,          (3.28)

Определяем сумму нагрузки на цилиндр, равномерного распределенной

по длине его бочки Q, H, по формуле

                                        (3.29)

.

Определяем сумму моментов сил относительно опоры  по формуле

,                                        (3.30)

где     R_A – реакция опоры, Н;

Отсюда определяем реакцию опоры А – R_A, H, по формуле

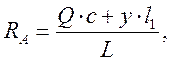                                    (3.31)

.

Определяем реакцию опоры В – R_B, H, по формуле

,                                              (3.32)

.

Реакции опор в дальнейшем будут использованы при расчете подшипников.

3.6 Расчет цилиндра

Определяем напряжение в корпусе цилиндра от давления пара σ_р, МПа, по формуле

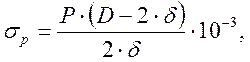                                   (3.33)

где     P – давление пара в цилиндре, МПа;

 - толщина стенки цилиндра, м;

Принимаем: Р = 5 атм = 5 · 10⁵;  = 0,025 м.

.

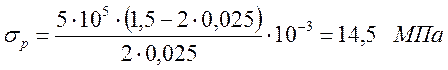Определяем максимальный изгибающий момент М, Н · м, по формуле

                                    (3.34)

.

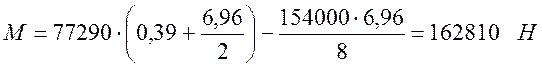Определяем момент инерции сечения бочки цилиндра I, м⁴, по формуле

,                                  (3.35)

.

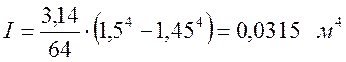Определяем момент сопротивления сечения бочки цилиндра W, м³, по формуле

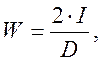                                              (3.36)

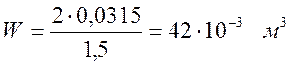
Определяем напряжение изгиба при максимальном изгибающем моменте σ_и , МПа, по формуле

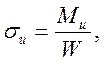                                              (3.37)

.

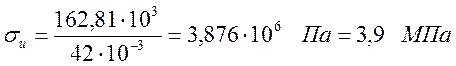Напряжение изгиба примерно в семь раз меньше допустимого, так как допустимое напряжение для чугунных цилиндров , т.е. .

Расчет сушильных цилиндров на критические обороты не производится, так как частота вращения цилиндра при его диаметре 1,5 м составляет 24,6 об/мин. (то есть, слишком мала для создания резонанса).

3.7 Расчет крышки цилиндра

Определяем наибольшее напряжение в крышке от давления пара в цилиндре σ_р, МПа, по формуле

                                 (3.36)

где     a – радиус крышки по окружности болтов, м;

b – радиус крышки в месте перехода цапфы на тарель, м;

δ₁ – толщина крышки, м.

Принимаем: a = 0,376 м; b = 0,18 м; δ₁ = 0,05 м.

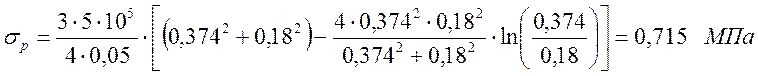
Определяем наибольшее напряжение в крышке от изгибающего момента σ_м, МПа, по формуле

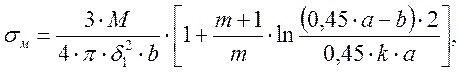                         (3.37)

где     m = 1/k – величина обратная коэффициенту Пуассона;

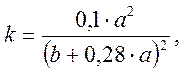                                  (3.38)

,

.

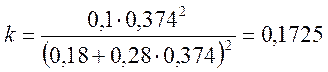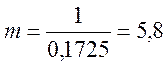Определяем изгибающий момент М, Н · м, по формуле

                                              (3.39)