Расчет оборудования для сушки целлюлозы (на примере сушильного цеха № 2 Братского ЛПК), страница 12

После чего производим построение эпюр изгибающих моментов (смотри рисунок 3.7).

Определяем, аналогично предыдущим расчетам, опорные реакции от сил, действующих в вертикальной плоскости R_Аy, R_Dy, Н, по формулам

,         (3.71)

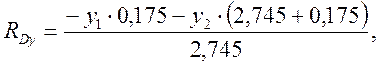                    (3.72)

,

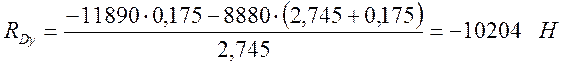,                    (3.73)

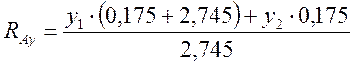          ,                   (3.74)

.

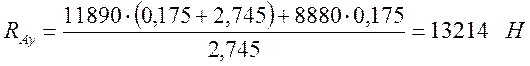Знак минус  показывает, что направление опорной реакции нужно поменять на противоположное направление (смотри рисунок 3.7).

Проверяем найденные реакции опор проекцией сил на ось y, Н, по формуле

,                            (3.75)

.

Проверка сошлась.

Определяем изгибающие моменты по участкам , Н∙м, по формулам

Участок I :

,                   (3.76)

.

Участок II :

,                          (3.77)

.

Участок III :

,                                         (3.78)

.

После чего производим построение эпюр изгибающих моментов (смотри рисунок 3.7).

          Производим построение крутящих моментов (смотри рисунок 3.7)

.

Определяем приведенные моменты в точках М_прi, Н·м, по формулам

,                                 (3.79)

,

                                        (3.80)

,

                                       (3.81)

.

Производим построение эпюры (смотри рисунок 3.7)

Определяем результирующие моменты в точках М_резi, Н·м, по формулам

,                               (3.82)

,                                        

,                                      (3.83)

,

,                                    (3.84)

.

3.11 Уточнённый расчет вала

Материал вала – сталь 40Х нормализованная,   и .

Примем, что нормальное напряжение от изгиба изменяются по симметричному циклу, а касательные от кручения – по от нулевому.

Определяем изгибающие моменты на наиболее нагруженную опору , Н∙м, по формулам

относительно оси х:

,                                    (3.85)

,

относительно оси у:

,                          (3.86)

.

Определяем результирующий изгибающий момент , , по формуле

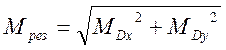,                                     (3.87)

.

          Определяем амплитуду номинальных напряжений изгиба , по формуле

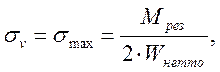                                       (3.88)

где     W_нетто – момент сопротивления нетто, мм².

          Принимаем: .

.

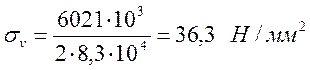          Определяем амплитуду и среднее напряжение цикла касательных напряжений  по формуле

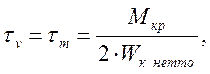                                         (3.89)

          Принимаем: .

.

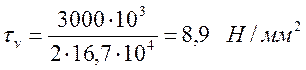          Определяем коэффициент запаса прочности , , по формулам

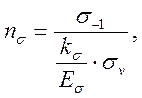                                        (3.90)

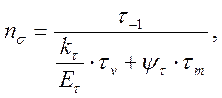                                       (3.91)

где , 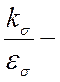эффективный коэффициент концентрации нормальных напряжений для валов с напрессованными деталями;

 коэффициент для принятых выше сталей принимаем;

 амплитуда отнулевого цикла, Н/мм²;

 среднее напряжение цикла касательного напряжения, Н/мм².

Принимаем:     .

,

.

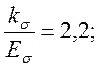
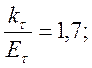
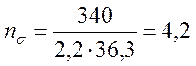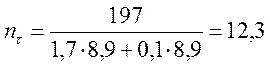Определяем общий коэффициент запаса прочности n, по формуле

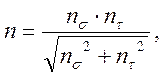                                     (3.92)

,

.

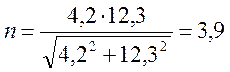Что вполне удовлетворяет условие прочности.

3.12 Проверка прочности шпоночного соединения

Для передачи вращающего момента применяем шпонку призматическую со скругленными торцами по ГОСТ 8788 – 68:

ведущий вал - 95 мм,  глубина паза t₁ = 10 мм. Момент на шестерни .

Определяем напряжение смятия шпонки под приводной шестерней , по формуле

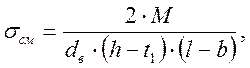                                   (3.93)

где     b – ширина шпонки, мм;

          h – высота шпонки, мм;

          l – длина шпонки, мм.

.

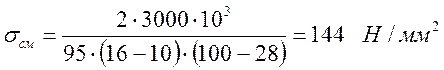          Принимаем: допустимый предел смятия при спокойном режиме работы .

.

          Определяем шпонки на срез , по формуле

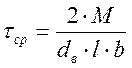,                                         (3.94)

,

.

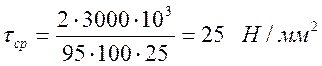Все условия выполняется.