Уравнениями (5) и (6) можно воспользоваться для экспериментального определения коэффициентов активности, так как из них следует, что
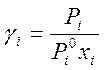 .
.
Для определения Рi можно использовать закон Дальтона, согласно которому Рi = уiР , где Р - общее давление пара, а уi -мольная доля i-го компонента в паре.
Критерий Рейдлиха-Кистлера
Критерий Рейдлиха-Кистлера применяют для проверки корректности определенных экспериментально коэффициентов активности.
Из
соотношения Гиббса-Дюгема для реального раствора 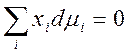 следует
следует
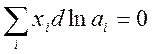 . Отсюда для двухкомпонентной системы x1dln(x1γ1) + x2dln(x2γ2) = 0. учитывая, что
dlnx = (1/x)dx, получаем dx1 + x1dlnγ1 + dx2 + x2dlnγ2 = 0. Поскольку x1 + x2 = 1, то dx1 + dx2 =0 и x1dlnγ1 + x2dlnγ2 = 0.
. Отсюда для двухкомпонентной системы x1dln(x1γ1) + x2dln(x2γ2) = 0. учитывая, что
dlnx = (1/x)dx, получаем dx1 + x1dlnγ1 + dx2 + x2dlnγ2 = 0. Поскольку x1 + x2 = 1, то dx1 + dx2 =0 и x1dlnγ1 + x2dlnγ2 = 0.
Полученные в эксперименте коэффициенты должны удовлетворять этому уравнению. Обычно для проведения проверки используют анализ проведения избыточной функции смешения для энергии Гиббса
![]() .
.
Отсюда 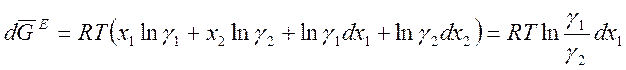 . Проинтегрируем это равенство в пределах
от х1 = 0 до х1 = 1:
. Проинтегрируем это равенство в пределах
от х1 = 0 до х1 = 1:
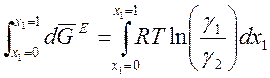 .
.
Значения
GE при х1 = 0 и х1
= 1 равны нулю, так как это избыточные потенциалы чистых веществ. Поэтому 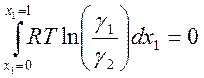 .
.
 Выполнение этого
соотношения,
которое называется Критерием Рейдлиха-Кистлера, эквивалентно
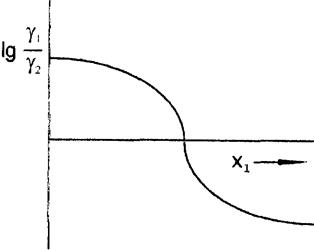
выполнению уравнения Гиббса—Дюгема. Справедливость критерия Рейдлиха-Кистлера обычно
проверяют графически, путём построения экспериментальной зависимости ln(γ1/γ2)
от х1. Суммарная площадь под построенной кривой должна
быть равна нулю, если экспериментальные величины уi определены правильно.
Выполнение этого
соотношения,
которое называется Критерием Рейдлиха-Кистлера, эквивалентно
выполнению уравнения Гиббса—Дюгема. Справедливость критерия Рейдлиха-Кистлера обычно
проверяют графически, путём построения экспериментальной зависимости ln(γ1/γ2)
от х1. Суммарная площадь под построенной кривой должна
быть равна нулю, если экспериментальные величины уi определены правильно.
Законы Коновалова
Исходя из условий фазового равновесия, можно показать, что если при добавлении к смеси при постоянной температуре одного из компонентов давление пара над раствором возрастает, т. е.
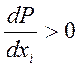 ,
,
|
|
то мольная доля
этого компонента в паре больше, чем в жидкости ![]() ,
т.е. пар
богаче тем компонентом, прибавление которого к раствору повышает общее
давление пара при постоянной температуре. Это утверждение есть первый закон Коновалова. Для бинарного
раствора во многих случаях справедливо более простое утверждение: пар богаче тем
компонентом, который имеет более высокое давление пара, или который кипит при более низкой
температуре. Однако, это неверно, если общее давление пара над раствором имеет
экстремум.
,
т.е. пар
богаче тем компонентом, прибавление которого к раствору повышает общее
давление пара при постоянной температуре. Это утверждение есть первый закон Коновалова. Для бинарного
раствора во многих случаях справедливо более простое утверждение: пар богаче тем
компонентом, который имеет более высокое давление пара, или который кипит при более низкой
температуре. Однако, это неверно, если общее давление пара над раствором имеет
экстремум.
Зависимость мольной
доли более
летучего компонента в паре y2, от мольной доли его в жидкости приведена
на рисунке (так называемая у-х
диаграмма). Прямая линия соответствует уравнению у2 = x2. Кривая зависимости состава
пара от состава жидкости лежит выше диагональной прямой, если 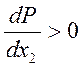
Если же давление пара над раствором
не меняется с изменением состава раствора, т.е. 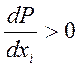 , то составы жидкости и пара совпадают (
, то составы жидкости и пара совпадают (![]() ). Эту зависимость выражает второй закон
Коновалова: в точках экстремума
кривых давление-состав при Т = const составы жидкости и
пара совпадают. Растворы, обладающие экстремумами давления пара, называются азеотропными.
Диаграмма у-х для таких систем имеет вид показанный на рисунке,
изображенном ниже. Точка А соответствует азеотропному раствору y2 = х2).
). Эту зависимость выражает второй закон
Коновалова: в точках экстремума
кривых давление-состав при Т = const составы жидкости и
пара совпадают. Растворы, обладающие экстремумами давления пара, называются азеотропными.
Диаграмма у-х для таких систем имеет вид показанный на рисунке,
изображенном ниже. Точка А соответствует азеотропному раствору y2 = х2).
|
|
Но часто необходимо знать зависимость температуры кипения растворов от их составов при постоянном давлении, т. е. необходимо рассматривать изобарическую диаграмму (Т-x).
|
|
|
|
|
Рис. Диаграмма состояния температура-состав для системы С2Н5ОН – ССl4 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.