Фазовые равновесия: Равновесие жидкость - пар в бинарных системах, страница 2

            Переход dn_iмолей компонента из одной фазы (‘) в другую (“) в рассматриваемых условиях вызывает изменение изобарного потенциала dG, которое складывается из изменений изобарных потенциалов обеих фаз dG’и dG”:

.

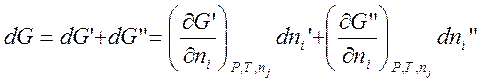            Так как dn_i’=-dn_i”, это соотношение можно переписать в виде

.

Если система находится в состоянии равновесия, то свобод­ная энергия системы достигает минимума и перенос бесконечно малого количества вещества из одной фазы в другую не меняетсвободную энергию системы. Как видно из последнего соотноше­ния, это возможно, только если μ_i" - μ_i'. Или, в случае равновесия нескольких фаз,

μ_i' = μ_i'' = μ_i''' =...

Таким образом, в состоянии равновесия химические потен­циалы каждого из компонентов одинаковы во всех фазах.

Фазовые равновесия в однокомпонентной системе.

В связи с постоянством состава однокомпонентной системы химический потенциал индивидуального вещества совпадает с мольной энергией Гиббса. В однокомпонентной системе условием равновесия между двумя фазами при постоянстве давления и температуры является равенство мольных энергий Гиббса компо­нентов в сосуществующих фазах. Если температура изменяется при постоянном давлении или давление изменяется при постоян­ной температуре, то равновесие нарушается и одна из фаз исчеза­ет.

Условие сосуществования двух фаз при одновременном из­менении давления Р и температуры Т задаётся уравнением Клапейрона

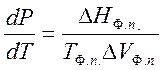, (1)

где ΔΗ_ф.п. - мольная энтальпия равновесного фазового перехода (например, испарения), ΔV_ф.п. - разность мольных объёмов фаз, находящихся в равновесии.

В случае равновесия жидкость-пар уравнение (1) можно уп­ростить, считая, что мольным объёмом жидкой фазы можно пренебречь по сравнению с мольным объёмом пара. Подставляя в уравнение (1) ΔV_ф.п. = (V_nap-V_ж) ≈ V_пар = RT/P, получаем уравнение Клаузиуса-Клапейрона

Полагая теплоту испарения постоянной величиной (что вполне допустимо в небольшом интервале температур), можно проинтегрировать уравнение (2):

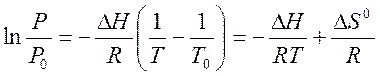Здесь Ρ₀ и Т₀ - фиксированные значения температуры и дав­ления, при которых возможно равновесие жидкость-пар. Если выбрать Ро = 1 атм, то Т₀ - это нормальная температура кипения, аΔS⁰ = ΔН⁰/ Т₀ - энтропия испарения при нормальной температу­ре кипения.

Уравнение даёт зависимость Р от Т на линии равновесия фаз. По этому уравнению можно рассчитать энтальпию испарения, исходя из значений давления пара при двух разных температурах Т и Т₀. Зависимость давления насыщенного пара от температуры в координатах (ΙnΡ)-(1/Τ), представляет собой прямую линию, из наклона которой можно определить ΔН_исп.

Фазовые равновесия в многокомпонентной системе. Растворы неэлектролитов.

Раствор - это гомогенная смесь переменного состава. Разли­чают жидкие и твёрдые растворы, при этом термин «раствор» не содержащий уточнений, относят к жидкой системе. Раствор называют идеальным, если при его образовании не изменяется объём, отсутствуют тепловые эффекты, а энтропия смешения такая же, как при смешении идеальных газов. Для идеального раствора выполняется закон Рауля - парциальное давление пара компонента Р_iпропорционально его мольной доле в растворе:

Р_i = Р_i°х_i ,

где Р_i° - давление пара чистого компонента при данной темпера­туре. В идеальных растворах закон Рауля выполняется для обоих компонентов во всём диапазоне составов.

Химический потенциал компонента в идеальном растворе связан с его мольной долей соотношением

μ_i =μ_i⁰+RΤ lnx_i .(3)

Рассмотрим равновесие идеальный жидкий раствор - насы­щенный пар, который будем считать идеальный газом. При равновесии химический потенциал i-го компонента в растворе равен его химическому потенциалу в паровой фазе. Так как химический потенциал компонента в смеси идеаль­ных газов μ_ι = μ_i° + RTln Р_i , то из соотношения (3) следует: