Фазовые равновесия: Равновесие жидкость - пар в бинарных системах, страница 3

. (4)

Отсюда 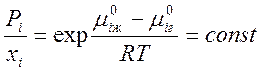 при постоянной Т. Таким образом, P_i= const ^.x_i , причём легко видеть, что const= P_i° . Видно, что закон Рауля является следствием соотношения (4).

Для бинарного раствора закон Рауля можно представить в следующем виде:

.

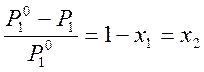Относительное понижение давление пара растворителя над раствором равно мольной доле x₂растворённого вещества. Общее давление пара над раствором равно сумме парциальных давлений:

,

т. е. давление пара линейно зависит от состава раствора.

Из закона Рауля следует, что зависимость общего давления пара от состава идеального раствора выражается прямой линией. В реальных предельно разбавлен­ных растворах для растворителя выполняется закон Рауля, а для растворённого вещества выполняется закон Генри:

Р₂=К_гх₂ ,

где К_г - константа Генри. В идеальных растворах закон Генри совпадает с законом Рауля ( К_г = Р₂° ). В реальных растворах могут наблюдаться различные отклонения от закона Рауля.

Поведение реального раствора тем существеннее не подчиняется законам идеальных растворов, чем больше различие между компонентами в отношении размера, формы и энергии взаимо­действия молекул. Для неидеальных растворов общее давление пара уже не является линейной функцией состава раствора.

Давление пара над реальным раствором может быть как больше аддитивной величины (положительное отклонение от закона Рауля), так и меньше (отрицательное отклонение).

Вид диаграмм Р-х (при Т = const) для реаль­ных растворов изображен на рис. 2. Причины отклонений от закона Рауля можно объяснить следующим образом: если разнородные молекулы в растворе взаимодействуют слабее, чем однородные, то переход компонентов раствора в газовую фазу облегчается по сравнению с   чистыми   жидкостями и наблюдается положительное отклонение от идеальности (вода-бензол, сероуглерод-ацетон, вода-метиловый спирт и т. д.). В обратном случае наблюдается отрицательное отклонение от закона Рауля (пиридин-уксусная кислота, ацетон-хлороформ и т. д.)

Рис. 2. Отклонение от закона Рауля для реальных растворов: / - положительное отклонение; 2 — отрицательное отклонение

Причинами более сильного взаимодействия молекул в рас­творе по сравнению с чистыми веществами могут быть образова­ние водородных связей, сольватация, образование химического соединения и т. д. Существуют растворы, в которых знак откло­нения от закона Рауля меняется с изменением концентрации.

Для реальных растворов уравнение (3) не выполняется. Для того, чтобы сохранить выражение для химического потенциала компонента в реальном растворе таким же, как в идеальном, Льюис предложил представить химический потенциал i-го вещества в виде

μ_i =μ_i⁰+RΤ lnа_i , (5)

где а_i - активность i-ro компонента в растворе; μ_i° - стандартный химический потенциал. Это выражение служит определением активности вещества в растворе. Величина активности опреде­ляется выбором стандартного состояния, в качестве которого для растворов неэлектролитов чаще всего выбирают чистое вещество (необходимо указать также его агрегатное состояние). При таком выборе стандартного состояния активность чистого компонента равна 1. Это такое же стандартное состояние, что и для идеально­го раствора.

В идеальном растворе а_i = х_i и уравнение (5) переходит в уравнение (3). Используя уравнение (5), можно для реального раствора получить термодинамические уравнения, которые будут иметь тот же вид, что и уравнения для идеального раствора, но место мольной доли компонента х_i в них будет занимать его активность a_i .

Введем коэффициент активности γ_i , связывающий актив­ность компонента с его мольной долей

γ_i =α_i/х_i .(6)

Величина y_iтоже определяется выбором стандартного со­стояния. Если за стандартное состояние выбрано чистое вещество, то коэффициент активности чистого вещества равен 1.