УРАВНЕНИЕ МИХАЭЛИСА -МЕНТЕН
Простейшей моделью для построения и обсуждения теорий ферментативной кинетики является кинетика односубстратных реакций. Хотя чаще всего в реакциях участвует не один, а большее число субстратов, реакцию можно рассматривать как односубстратную, если второй субстрат присутствует в очень большой концентрации. Большинство получаемых выводов можно использовать непосредственно при рассмотрении более сложных ферментативных реакций.
Как уже упоминалось, концентрация субстрата является одним из наиболее важных факторов, определяющих скорость ферментативной реакции.
В начале XX столетия Л. Михаэлисом и М. Ментен было предложено простейшее кинетическое выражение для скорости ферментативной односубстратной реакции.
Схема ферментативного процесса записывается следующим образом:
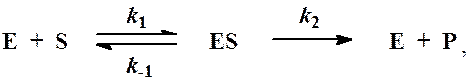
где Е - фермент; S - субстрат, подвергающийся ферментативной реакции; Р - образующийся в результате продукт;
ES - фермент-субстратный комплекс; k1, k-1, k2- константы скорости индивидуальных реакций.
Уравнение скорости ферментативной реакции, выведенное Михаэлисом и Ментен, предположивших, что превращение субстрата происходит только в переходном фермент-субстратном комплексе, основывается на двух предпосылках.
1. Реакция между ферментом и субстратом находится в равновесии. Это условие выполняется, если скорость распада комплекса на свободный фермент и субстрат значительно больше скорости распада его до свободного фермента и продукта (k-1 >> k2).
2. Концентрация свободного субстрата остается практически постоянной в течение начального периода реакции, тогда концентрация субстрата [S] может быть принята равной полной концентрации субстрата [So]. Это условие выполняется, если полная концентрация субстрата значительно больше полной концентрации фермента, как это обычно имеет место при кинетических исследованиях.
При высокой каталитической активности фермента реальное значение концентрации фермент-субстратного комплекса отличается от его значения в условиях равновесия. Для анализа кинетики реакции с учетом этого обстоятельства Бриггс и Холдейн предложили дополнить теорию Михаэлиса - Ментен условием стационарного состояния.
Согласно этому условию в любой момент реакции скорости образования и распада комплекса ES практически равны, так что концентрация комплекса [ES] может считаться постоянной (квазистационарной) в течение короткого периода времени, необходимого для измерения скорости. В течение более продолжительного периода времени концентрация комплекса [ES] будет изменяться по ходу реакции в связи с падением концентрации субстрата, но скорость изменения ее всегда будет существенно меньше, чем скорость ферментативной реакции.
Скорость образования комплекса ES равна k1[E][S], а скорость распада ES равна сумме двух величин – скорости распада ES до Е и S, т. е. k-1 [ES], и скорости распада ES до Е и продукта P (k2 [ES]).
Для стационарного состояния, при котором
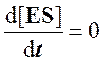 ,
,
получаем:
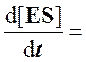 k1[E][S]
– (k-1 + k2)·[ES]
= 0
k1[E][S]
– (k-1 + k2)·[ES]
= 0
или
![]()
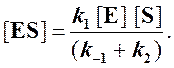 (1)
(1)
Из уравнения материального баланса для фермента
[Eo] = [E] + [ES],
где [Eo] ─ его начальная концентрация, а [E] ─ текущая концентрация свободного, не связанного в фермент-субстратный комплекс белка, можно записать
[E] = [Eo] ─ [ES]
и подставить в выражение (1):
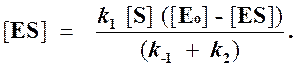
Отсюда концентрация ES равна
[ES] = 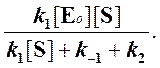
Тогда начальная скорость ферментативной реакции, измеряемая по скорости образования продукта Р, равна
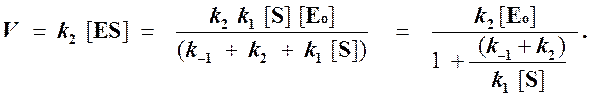 (2)
(2)
Если ввести обозначения Vmax = k2[Eo] (максимальная скорость ферментативной реакции) и
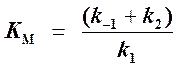 (константа Михаэлиса),
(константа Михаэлиса),
то выражение (2) можно записать в следующем виде:
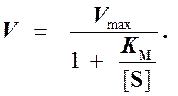 (3)
(3)
Выражение (3) называется уравнением Михаэлиса -Ментен и описывает зависимость скорости односубстратной ферментативной реакции от концентрации субстрата. Из этого уравнения видно, что при увеличении концентрации субстрата (при неизменной концентрации фермента) скорость реакции стремится к предельному значению, равному Vmax.
При выводе уравнения Михаэлиса - Ментен, кроме вышеперечисленных, принимается во внимание еще несколько не совсем реальных допущений, таких как:
1) отсутствие образования значимого количества комплекса ЕР и других форм фермента;
2) необратимость второй стадии реакции, т. е. образования продукта Р. Это связано с тем, что мы рассматриваем только начальную скорость процесса, когда обратной реакцией из-за фактического отсутствия продукта еще можно пренебречь;
3) связывание с активным центром на каждой субъединице фермента только одной молекулы субстрата;
4) использование для всех реагирующих веществ вместо активностей их концентраций.
Если k2 значительно меньше k-1, то этим членом в
выражении константы Михаэлиса можно пренебречь, и КM становится равной
отношению ![]() , а это есть Кd (константа диссоциации
фермент-субстратного комплекса):
, а это есть Кd (константа диссоциации
фермент-субстратного комплекса):
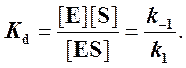
Таким образом, являясь аналогом константы диссоциации фермент-субстратного комплекса ES, константа Михаэлиса характеризует сродство фермента к субстрату. Чем ниже КM, тем выше сродство.
На рис. 1 приведено графическое изображение уравнения Михаэлиса - Ментен.
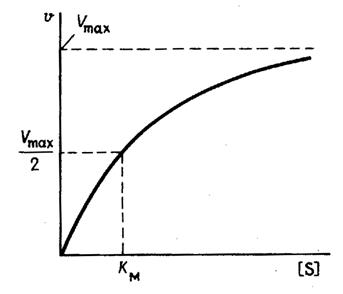
Рис. 1.Зависимость скорости ферментативной реакции от концентрации субстрата
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.