Уравнение Михаэлиса-Ментен. Ингибирование ферментов, страница 2

Кривая зависимости начальной скорости ферментативной реакции от концентрации субстрата представляет собой равнобочную гиперболу, где величина скорости реакции V асимптотически достигает V_max с возрастанием концентрации субстрата [S]. Определение достоверной величины констант К_M и V_max по этому графику затруднено из-за сложностей экстраполяции.

Из выражения (3) и рис. 1 видно, что К_M численно равна той концентрации субстрата, при которой значение скорости реакции достигает половины от V_max.

Для удобства расчетов V_max и К_M уравнение Михаэлиса - Ментен преобразуют так, чтобы экспериментальные точки лежали на прямой линии. Существует несколько графических линейных преобразований этого уравнения:

1) Метод Лайнуивера - Бэрка, или график двойных обратных величин.

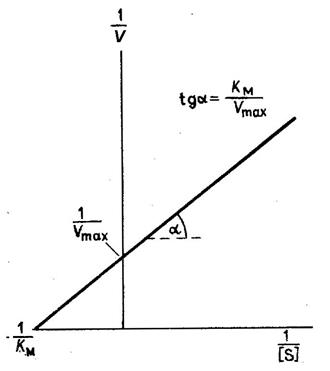
Рис. 2. Зависимость скорости реакции от концентрации субстрата (график Лайнуивера - Берка, или график двойных обратных величин)

Уравнение Михаэлиса - Ментен приводится к следующему виду:

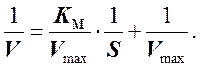
Если построить график в координатах от , как это изображено на рис. 2, то он будет представлять собой прямую, пересекающую ось абсцисс в точке 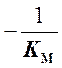, а ось ординат в точке .

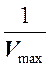2) Метод Иди - Хофсти.

В этом случае уравнение Михаэлиса - Ментен преобразуют к виду

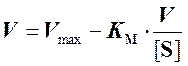                                     (4)

и строят график зависимости Vот  (рис. 3).

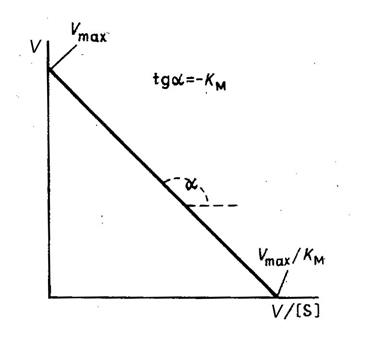
Рис. 3. Зависимость скорости реакции от концентрации субстрата в координатах Иди - Хофсти

Величину К_M получают путем деления длины отрезка, отсекаемого на оси ординат, на длину отрезка, отсекаемого на оси абсцисс.

3) Метод Эйзенталя и Корниш-Боудена.

Этот метод не предусматривает построения графика по экспериментальным точкам. Уравнение (4) преобразуют в виде

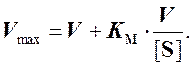
Отсюда следует, что для любой пары значений [S] и V можно построить зависимость V_max от K_M, которая представляет собой прямую с наклоном, равным , и отрезками, отсекаемыми на осях K_M и V_max, соответственно равными [S] и V.

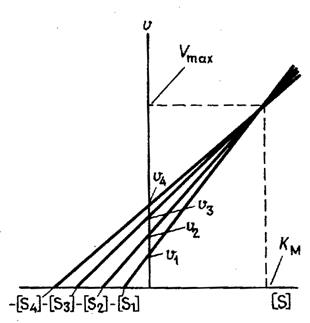
Рис. 4.Определение констант уравнения Михаэлиса - Ментен с помощью метода Эйзенталя и Корниш-Боудена

Величины V и [S] откладывают на вертикальной и горизонтальной осях соответственно и через каждую пару точек проводят прямую (рис. 4). Если подобным образом провести прямые для нескольких пар величин [S] и V, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения K_M и V_max, удовлетворяющие всем парам [S] и V. Если не все прямые пересекаются строго в одной точке, то оптимальные значения  К_M и V_max получают по их среднему значению.

При исследовании влияния ошибок в определении начальных скоростей на получаемые значения К_M  и V_max было установлено, что, хотя до сих пор метод Лайнуивера - Бэрка предпочтительно используется при расчете параметров уравнения, этот метод является наименее надежным из рассмотренных выше. Метод Иди - Хофсти наиболее чувствителен к отклонению от линейности. В настоящее время данные ферментативной кинетики обрабатываются быстрее и более объективно с помощью вычислительной техники.

ИНГИБИРОВАНИЕ ФЕРМЕНТОВ

Скорость ферментативных реакций может зависеть от присутствия некоторых соединений, специфичных для каждого фермента. Одни из этих соединений, ускоряющие каталитические процессы, являются активаторами ферментативных процессов. Вещества, замедляющие эти процессы, представляют собой ингибиторы ферментов.

Ингибиторы ферментативных реакций могут быть обратимыми и необратимыми.

В случае необратимых ингибиторов происходит, как правило, образование ковалентной связи между ингибитором и существенным для проявления каталитической активности участком белка (химическая модификация фермента), что и приводит к необратимой инактивации. Необратимый ингибитор может также нарушать конформацию молекулы фермента, вызывая его денатурацию.

Если удаление ингибитора приводит к восстановлению каталитической активности белка, то такой ингибитор является обратимым. В зависимости от места связывания обратимого ингибитора различают конкурентное, неконкурентное и бесконкурентное ингибирование.

1.  Конкурентное ингибирование