Уравнение Михаэлиса-Ментен. Ингибирование ферментов, страница 5

Рис. 11. Зависимость скорости ферментативной реакции от концентрации субстрата в отсутствие и в присутствии бесконкурентного ингибитора в координатах Иди - Хофсти

В координатах Эйзенталя и Корниш-Боудена (рис.7, в) при бесконкурентном ингибировании наблюдается смещение точки пересечения прямых, построенных в координатах К_M; V_max, вниз (V_max заменяется на V_maxI) и влево (вместо К_M получаем К_Mi), что говорит об одновременном уменьшении максимальной скорости ферментативной реакции и константы Михаэлиса.

В случае односубстратных реакций бесконкурентное ингибирование наблюдается крайне редко.

Метод графов для получения уравнения скорости ферментативной реакции

Анализ кинетических схем можно существенно упростить путем применения теории графов. Эта теория была развита в работах Кинга и Альтмана. В качестве примера рассмотрим применение этой теории для анализа скорости ферментативной реакции.

Граф – это совокупность точек (вершин) и соединяющих их линий. Если линии имеют направление (ориентированы), то их называют дугами (ветвями); неориентированные линии называются ребрами.

Каждой ветви графа приписывается численное значение, т. е. величина ветви, что является аналогом константы скорости (например, а и b в приведенных ниже уравнениях 1-3).

Непрерывная совокупность ветвей в каком-либо направлении, при котором ни одна из вершин не встречается более одного раза, дает путь графа.

Дерево – это совокупность нескольких вершин, соединенных ветвями.

Если каждая вершина графа соединена хотя бы с одной другой, такой граф называется связанным.

Для анализа кинетической схемы одну из вершин графа выбирают в качестве базовой (базы).

Базовое дерево – это совокупность всех ветвей, проходящих через все вершины графа и направленных к базе. Выбор базы во многом является произвольным и определяется опытом исследователя. В качестве базы обычно выбирают ту вершину,  которая образует наиболее большое базовое дерево, при этом оно не должно содержать циклов (не должно начинаться и оканчиваться в одной и той же вершине).

Сумма величин всех базовых деревьев, направленных к одной базе, называется определителем базы или базовым определителем графа. Для определения скорости ферментативной реакции требуется вычисление всех базовых определителей графа. Некоторые свойства графа позволяют упростить их вычисление.

Так, теория графов предполагает, что:

1) Кратные ветви складываются. Если вещество А превращается в вещество В с помощью двух химических реакций с константами скорости а и b соответственно, то путь

А  В равен (а+b):

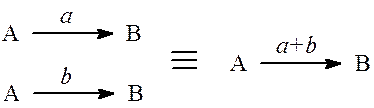
2) Величины ветвей, направленных к одной базе, перемножаются. Если вещества А и С превращаются в вещество В:

 

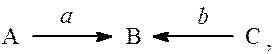
то путь () равен аb.

3) Путь графа равен произведению величин всех ветвей этого пути:

 

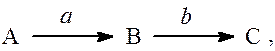
путь (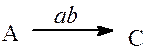) равен аb.

Стационарная скорость ферментативной реакции с помощью метода графов записывается следующим образом:

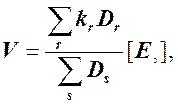                                      (8)

где D_S – базовые определители всех состояний фермента; D_r – базовые определители состояний фермента, приводящих к образованию продукта; k_r – константы скоростей стадий, приводящих к образованию продукта.

Запишем с помощью метода графов стационарную скорость реакции для схемы

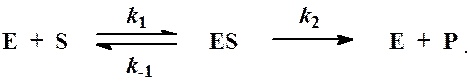
Удобнее представить эту схему следующим образом:

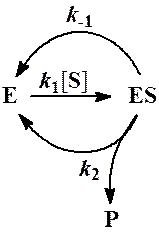
Так как параллельные ветви графа складываются, то граф эквивалентен следующему:

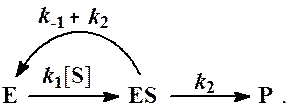
В этом графе есть два состояния фермента - Е и ES. Поскольку продукт Р образуется из ES, то базовый определитель, приводящий к образованию продукта, равен D_r = D_ES = k₁[S]. Для другого состояния фермента - Е имеется другой базовый определитель этого графа - D_S = k_-1+k₂.

Константа скорости образования продукта равна k_r = k₂.

Согласно уравнению (8) стационарная скорость ферментативной реакции определяется следующим образом:

,

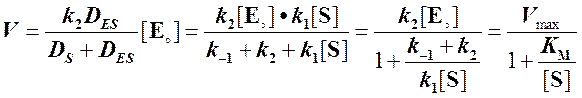что соответствует уравнению Михаэлиса - Ментен (выражение (3)).

С использованием метода графов можно вывести уравнение скорости для любого более сложного механизма ферментативной реакции.