Симплекс-метод для отыскания опорного решения. Примеры. Симплекс-метод для отыскания оптимального решения. Примеры

Вычислительная математика

   Специальность ПО         

4-й семестр

Конспект лекций

Лекция 10

            Симплекс-метод для отыскания опорного решения. Примеры. Симплекс-метод для отыскания оптимального решения. Примеры.

1.  Симплекс-метод для отыскания опорного решения.

            Итак, мы приступаем к конкретному описанию симплекс-метода.  Напомним обозначе-ния задачи (ср.Лекцию 8):

           

при ограничениях

            .

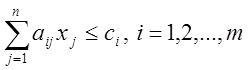Здесь  - переменные (аргументы), а , - константы. В соответствии с предварительной подготовкой, о которой речь шла в конце Лекции 9,  пере-менные  либо неотрицательны, либо свободны – других нет.

            Построим Рабочую таблицу для симплекс-метода:

		...		1
		...
...	...		...	...
		...
z=				0

                                              Рабочая таблица

восстановление условия задачи по такой таблице очевидно; переменные

  в этой ситуации, согласно условию ОЗЛП,  должны быть неотрицатель-ны.

            Вычеркнем из этой таблицы строки, соответствующие неравенствам .

            Выразим с помощью МЖИ в рабочей таблице все свободные переменные через неотри-цательные переменные , насколько это возможно.  Строчки полученной таблицы, слева от которых окажутся свободные переменные, удалим из таблицы и сохраним для дальнейших дей-ствий. Если после этого над таблицей останется хоть одно свободное , то надо будет рассмо-треть коэффициент при этом  в целевой функции ; если этот коэффициент отли-чен от нуля, то ОЗЛП не имеет решения и дальнейших действий не требуется. Если же в целе-вой функции коэффициент при свободной неизвестной оказался равным нулю, то в рабочей таблице следует удалить столбец, над которым указана эта свободная переменная . После этого следует приступить к дальнейшим действиям с полученной в результате таблицей. Над ее столбцами теперь будут указаны некоторые из переменных . Для определенности будем считать, что таблица имеет следующий вид:

		...		1
		...	...	bn+1n+1...
...	...	...	...	...
		...
		...

                                           Рабочая таблица 1

В ближайших действиях будет несущественно, каков именно вид z-строки. Поэтому Рабочую таблицу 1 естественно записывать без этой строки:

		...		1
		...	...	bn+1n+1...
...	...	...	...	...
		...

                                         Рабочая таблица 2

Заметим, что у нас возникли Рабочая таблица, Рабочая таблица 1 и Рабочая таблица 2. Описываемую ниже процедуру анализа называют поиском опорного решения, т.е. поиском точки, которая удовлетворяет всем ограничениям и, по крайней мере, одно из них обращает в равенство.

            Шаг 1. Просматривается правый столбец Рабочей таблицы 2. Если все его элементы неотрицательны, то задача о поиске опорного решения решена: опорным решением служит точка . Если же среди элементов правого столбца  есть отрицательный, то переходим к следующему шагу.

            Шаг 2. Пусть . Просматриваем строку № i. Если среди ее элементов все, кроме крайнего правого, неотрицательны, то условие задачи противоречиво и, следовательно, нет опорного (и любого другого) решения. В этом случае процедура закончена. Если же отрица-тельное число в этой строке нашлось (кроме крайнего правого), то переходим к следующему шагу.

            Шаг 3. Пусть . Мы найдем сейчас ненулевой элемент, который выполнит роль разрешающего при модифицированном жордановом исключении в Рабочей таблице 2. Столбец этого элемента уже найден - это столбец  № . Рассмотрим все те дроби 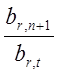 , которые больше или равны нулю, причем если такая дробь равна нулю, то в рассмотрение она включается лишь при условии, что ее знаменатель положителен. Выберем среди этих дробей минимальную. Пусть это будет, скажем, дробь 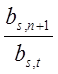. Искомым разрешающим элементом объ-является .

            После этого надо возвратиться к Шагу 1.