Симплекс-метод для отыскания опорного решения. Примеры. Симплекс-метод для отыскания оптимального решения. Примеры, страница 4

            Исключаем свободные неизвестные, а потом соответствующие им строки не будем записывать в дальнейшие таблицы. Первый разрешающий элемент выделен в нижеследующей таблице серым фоном:

	-x1	-x2	1
y1=	-1	-2	1
y2=	-2	-1	-4
y3=	-1	1	1
y4=	-1	4	13
y5=	4	-1	23
z=	3	-6	0

Получем:

	- y1	-x2	1
x1=	-1	2	-1
y2=	-2	3	-6
y3=	-1	3	0
y4=	-1	6	12
y5=	4	-9	27
z=	3	-12	3

Теперь исключим x₂  с помощью разрешающего элемента, выделенного серым цветом:

	- y1	-x2	1
x1=	-1	2	-1
y2=	-2	3	-6
y3=	-1	3	0
y4=	-1	6	12
y5=	4	-9	27
z=	3	-12	3

Получим:      

	- y1	- y2	1
x2=	-2/3	1/3	-2
y3=	1	-1	6
y4=	3	-2	24
y5=	-2	3	9
z=	-5	4	-21

И, таким образом, получается следующая таблица для дальнейших действий:

	- y1	- y2	1
y3=	1	-1	6
y4=	3	-2	24
y5=	-2	3	9
z=	-5	4	-21

Здесь правый столбец уже положителен и, следовательно, опорное решение есть: y₁= y₂=0. Поэтому переходим сразу к поиску решения оптимального.

            Просматриваем строку целевой функции. Если в ней не окажется отрицательных чисел (кроме, возможно, последнего справа), то задача решена. Но в нашем примере есть отрицатель-ное число - это -5. Следовательно, просматриваем столбец этого числа, отыскивая в нем поло-жительные числа. Если их не окажется, то задача решена - функция неограниченна. Но в нашем примере положительные числа в этом столбце есть. Поэтому надо рассмотреть дроби вида 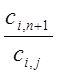>0 и выбрать из них минимальную. В нашем примере - это дроби 6/1 и 24/3. Следователь-но разрешающим элементом будет выделенный серым фоном в нижеследующей таблице:

	- y1	- y2	1
y3=	1	-1	6
y4=	3	-2	24
y5=	-2	3	9
z=	-5	4	-21

В результате модифицированного жорданова исключения получаем:

	- y3	- y2	1
y1=	1	-1	6
y4=	-3	1	6
y5=	2	1	21
z=	5	-1	9

Вновь в строке целевой фуекции отрицательный элемент, вновь просматриваем

его столбец и ищем минимум среди чисел 6/1, 21/1. Разрешающий элемент выделен серым фоном в нижеследующей таблице:

	- y3	- y2	1
y1=	1	-1	6
y4=	-3	1	6
y5=	2	1	21
z=	5	-1	9

Заметим, что при модифицированном жордановом исключении таблица заполняется не одно-моментно, а поэлементно. Нетрудно заметить, что целесообразно заполнять таблицу, начиная с наружного угла, а именно (в данном примере):

	- y3	- y4	1
y1=			12
y2=			6
y5=			15
z=	2	1	15

Теперь строка целевой функции положительна и, следовательно, ответ найден:

максимум целевой функции равен 15. Он достигается при y₃=y₄=0 и, следовательно y₁=12, y₂=6, y₅=15, x₂=4, x₁=3.