Симплекс-метод для отыскания опорного решения. Примеры. Симплекс-метод для отыскания оптимального решения. Примеры, страница 3

Вновь просматриваем правый столбец в поисках отрицательного элемента. На-ходим -1. Просматриваем строку этого элемента в поисках иных отрицательных чисел. Находим -1. Столбец этого числа, т.е. второй столбец будет разрешаю-щим. Строим неотрицательные дроби: -1/(-1). И больше нет. Строка, соответст-вующая этой дроби будет разрешающей. Следовательно, предстоит произвести модифицированное жорданово исключение с разрешающим элементом, кото-рый выделен в нижеследующей таблице серым фоном:

	-y2	-x2	-x3	1
y1=	1	-3	4	2
y3=	2	-1	-3	-1
y4=	0	-3	-3	2
y5=	2	-3	0	4

Получаем:

	-y2	-y3	-x3	1
y1=	-5	-3	13	5
x2=	-2	-1	3	1
y4=	-6	-3	6	5
y5=	-4	-3	9	7

Вновь просматриваем правый столбец в поисках отрицательного элемента. Теперь такого нет. Следовательно, опорное решение - это точка:

.

Чтобы выразить эту точку в исходных переменных -  , - надо просмотреть таблицы в обратном порядке, начиная с последней. Из последней таблицы вид-но, чему равно  (из строчки, которая начинается с ): =1. Из предыдущей таблицы находим: y₁=5. Теперь из основной таблицы можно найти: x₁=0. Таким образом, опорное решение найдено: это точка (0,1,0).

3.  Симплекс-метод для отыскания оптимального решения.

Итак, будем считать, что имеется ОЗЛП, что ее данные приспособлены уже к примене-нию симплекс-метода и что, более того, уже отыскали опорное решение. В приведенном выше примере этот поиск происходил без реального присутствия целевой функции, хотя на практике, конечно, целевая функция присутствует и соответствующая ей строка полностью участвует в  модифицированных жордановых исключениях. Будем поэтому считать, что перед переходом к поиску оптимального решения рабочая таблица имеет вид:

	y1	...	yn	1
yn+1=	cn+1,1	...	cn+1,n	cn+1,n+1
...	...	...	...	...
ym=	cm,1	...	cm,n	cm,n+1
z=	Q1	...	qn	Q

В этой таблице правый столбец не содержит отрицательных чисел (кроме, быть может, Q) и опорное решение - это точка y₁=...= y_n=0.

            Опишем действия вновь по шагам.

            Шаг 1. Просматриваем  z-строку. Если в ней нет отрицательных чисел (кроме, возможно, числа Q, то задача решена: максимум целевой функции является число Q, а точкой максимума - точка , которую надо переписать в исходных переменных. Если же среди упомя-нутых чисел есть отрицательное, скажем , то переходим к следующему шагу.

            Шаг 2. Просматриваем столбец отрицательного коэффициента .Если в этом столбце все числа отрицательны или равны нулю, то задача решена: целевая функция неограничена. Ес-ли же в этом столбце есть положительные числа, то переходим к следующему шагу.

            Шаг 3. Просматриваем все дроби 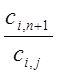, удовлетворяющие неравенству 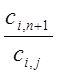>0 (обра-щаем внимание: строго больше нуля!). Выбираем из них минимальную и фиксируем номер строки , которому этот минимум соответствует. Элемент  принимается за разрешаю-щий в модифицированном жордановом исключении, которое и проводится. После этого переходим к Шагу 1.

            Можно доказать, что за конечное число проходов по указанным трем шагам оптималь-ное решение (или его отсутствие) будет установлено.

            Подчеркнем в заключение еще раз: если в процессе решения возникает таблица, которая уже была раньше («зацикливание»), то надо вернуться назад и при выборе последнего миниму-ма взять другой минимум.

4.Пример отыскания оптимального решения.

Рассмотрим в заключение пример полного решения ОЗЛП. Итак,

найти максимум функции

z=-3x₁+6x₂

при условиях:

y₁=x₁+2x₂+10,

y₂=2x₁+x₂-40,

y₃=x₁-x₂+10,

y₄=x₁-4x₂+130,

y₅=-4x₁+x₂+230.

Таким образом, здесь только две переменных - x₁, x₂ - и обе являются свободными. Построим рабочую таблицу:

	-x1	-x2	1
y1=	-1	-2	1
y2=	-2	-1	-4
y3=	-1	1	1
y4=	-1	4	13
y5=	4	-1	23
z=	3	-6	0